Radial Basis Functions Interpolation

Download Code

This is a set of Matlab functions to interpolate scattered data with Radial Basis Functions (RBF).

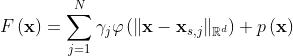
$F \left( \mathbf{x} \right) = \sum_{j=1}^N \gamma_j \varphi \left( \| \mathbf{x} - \mathbf{x}_{s, j} \|_{\mathbb{R}^d} \right) + p \left( \mathbf{x} \right)$

Getting Started

y = RBFinterp(xs, ys, x, RBFtype, R)

interpolates to find y, the values of the function y=f(x) at the points x.

Xs must be a matrix of size [N,Dx], with N the number of data points and Dx the dimension of the points in xs and x.

Ys must be a matrix of size [N,Dy], with N the number of known values at points in Xs, and Dy the dimension of the y values.

X must be a matrix of size [M,Dx], with M the number of query points.

RBFtype specifies the radial basis functions (RBF) to be used.

The available global support RBFs are:
- ‘R1’ - linear spline
- ‘R3’ - cubic spline
- ‘TPS2’ - thin plate spline
- ‘Q’ - quadric
- ‘MQ’ - multiquadric
- ‘IMQ’ - inverse multiquadric
- ‘IQ’ - inverse quadric
- ‘GS’ - Gauss

RBF name	Abbreviation	$\varphi \left( r \right)$
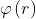Linear spline	R1	$\epsilon r$
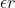Cubic splie	R3	$\left( \epsilon r \right)^3$
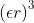Thin plate spline	TPS2	$\left( \epsilon r \right)^2 \log\left( \epsilon r \right)$$
Quadric	Q	$1 + \left( \epsilon r \right)^2$
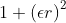Multiquadric	MQ	$\sqrt{1 + \left( \epsilon r \right) ^2}$
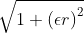Inverse multiquadric	IMQ	$\frac{1}{\sqrt{1 + \left( \epsilon r \right) ^2}}$
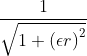Inverse quadric	IQ	$\frac{1}{ 1 + \left( \epsilon r \right) ^2 }$
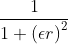Gauss	GS	$e^{-\left(\epsilon r \right)^2}$

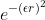The available compact support RBFs are (see Wendland H., Konstruktion und Untersuchung radialer Basisfunktionen mit kompaktem Träger. PhD thesis, Göttingen, Georg-August-Universität zu Göttingen, Diss, 1996):
- ‘CP_C0’
- ‘CP_C2’
- ‘CP_C4’
- ‘CP_C6’
- ‘CTPS_C0’
- ‘CTPS_C1’
- ‘CTPS_C2a’
- ‘CTPS_C2b’

Compact support functions have the form

$\varphi \left( \xi = \frac{r}{R} \right) = \begin{cases} f \left( \xi \right), & 0 \leq \xi \leq 1 \\ 0, & \xi > 1 \end{cases}$

RBF name	$\varphi \left( \xi \right)$
$\text{CP } \mathcal{C}^0$	$\left( 1 - \xi \right)^2$
$\text{CP } \mathcal{C}^2$	$\left( 1 - \xi \right)^4 \left( 4 \xi + 1 \right)$
$\text{CP } \mathcal{C}^4$	$\left( 1 - \xi \right)^6 \left( \frac{35}{3} \xi^2 + 6 \xi + 1 \right)$
$\text{CP } \mathcal{C}^6$	$\left( 1 - \xi \right)^8 \left( 32 \xi^3 + 25 \xi^2 + 8 \xi + 1 \right)$
$\text{CTPS } \mathcal{C}^0$	$\left( 1 - \xi \right)^5$
$\text{CTPS } \mathcal{C}^1$	$1 + \frac{80}{3} \xi^2 - 40 \xi^3 + 15 \xi^4 - \frac{8}{3} \xi^5 + 20 \xi^2 \log \xi$
$\text{CTPS } \mathcal{C}^2_a$	$1 - 30 \xi^2 - 10 \xi^3 + 45 \xi^4 - 6 \xi^5 - 60 \xi^3 \log \xi$
$\text{CTPS } \mathcal{C}^2_b$	$1 - 20 \xi^2 + 80 \xi^3 - 45 \xi^4 - 16 \xi^5 + 60 \xi^4 \log \xi$

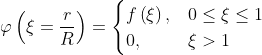
R is either the support radius for the compact support RBFs or a parameter to make the distance values dimensionless for the global support RBFs.

[fPar, M] = RBFparam(xs, ys, RBFtype, R)

returns the weights in the RBF summation and the polynomial coefficients in a column vector fPar by solving a linear system

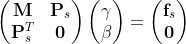
$\begin{pmatrix} \mathbf{M} & \mathbf{P}_s \\ \mathbf{P}_s^T & \mathbf{0} \end{pmatrix} \begin{pmatrix} \mathbf{\gamma} \\ \mathbf{\beta} \end{pmatrix} = \begin{pmatrix} \mathbf{f}_s \\ \mathbf{0} \end{pmatrix}$

[y] = RBFeval(xs, x, fPar, RBFtype, R)

returns the values of the interpolation weighted function at points x by performing the matrix-vector product

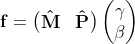
$\mathbf{f} = \begin{pmatrix} \mathbf{\hat{M}} & \mathbf{\hat{P}} \end{pmatrix} \begin{pmatrix} \mathbf{\gamma} \\ \mathbf{\beta} \end{pmatrix}$

Running the example

An example case can be run just by typing in the Matlab command line

test

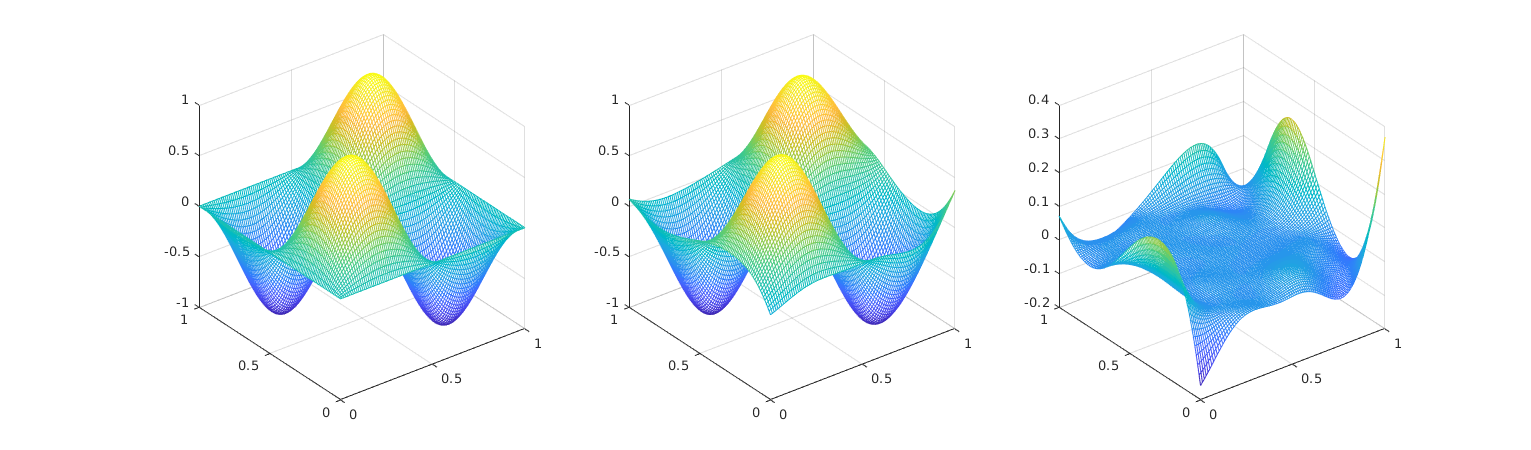
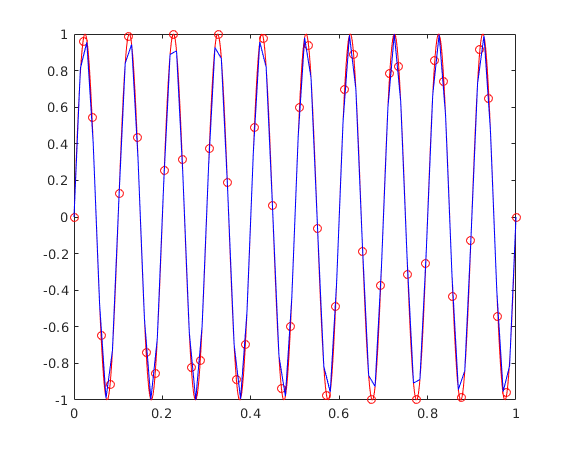
References

Beckert, Armin and Wendland, Holger. Multivariate interpolation for fluid-structure-interaction problems using radial basis functions. Aerospace Science and Technology, 5 (2), p. 125-134, 2001.
Wendland, Holger. Konstruktion und Untersuchung radialer Basisfunktionen mit kompaktem Träger}. PhD thesis, Göttingen, Georg-August-Universität zu Göttingen, Diss, 1996.
De Boer, A and Van der Schoot, MS and Bijl, Hester. Mesh deformation based on radial basis function interpolation. Computers & structures, 85 (11-14), p. 784-795, 2007.
Biancolini, Marco Evangelos. Fast Radial Basis Functions for Engineering Applications. Springer, 2018.

Multilevel Selective Harmonic Modulation via Optimal Control

The Multilevel Selective Harmonic Modulation problem is recast under the perspective of optimal control

Authors: Jesus Oroya, Carlos Esteve, Umberto Biccari - 25 March 2021

Opening the black box of Deep Learning

The aim is then to open the black box of Deep Learning, and try to gain an intuition of what are these models doing. One of the most succesful mathematical theories in recent years has been connecting Deep Learning with Dynamical Systems.

Author: Sergi Andreu - 22 March 2021

Points of Interest Extraction and Prediction of Next Locations

In this project we tried first working on finding an algorithm that can help us define the points of interest of the users we have in the dataset. For that we implement an algorithm that can identify the users stop points.

Author: Aicha Karite - 10 March 2021

Touchdown localization for the MEMS problem with variable dielectric permittivity

In this tutorial we study the localization of touchdown points in a mathematical model for micro-electro-mechanical systems (MEMS) with variable dielectric permittivity. We consider a device consisting of two conducting plates, connected to an electric circuit. The upper plate is rigid and fixed while the lower one is elastic and fixed only at the boundary. When a voltage (difference of potential between the two plates) is applied, the lower plate starts to bend and, if the voltage is large enough, the lower plate eventually touches the upper one. This is called touchdown phenomenon and our aim is to control the localization of touchdown points in the device by a suitable choice of the dielectric permittivity of the material.

Author: Carlos Esteve - 30 September 2019

Work Packages ≻ Other Topics ≻