A numerical method for solving an age structured virus model

Download Code

The aim of this tutorial is to give a numerical method for solving an age structured virus model.

Introduction

The virus infection mathematical models are proposing and studying for a long time (see for example C.L. Althaus, R.J. DE Boer [1] and F. Brauer, C. Castillo-Chavez [2]. In particular case of an HIV infection model (see for P. W. Nelson and al. [6]), the corresponding model is usually divided into three classes called uninfected cells, $T$, infected cells, $i$ and free virus particles, $V$.

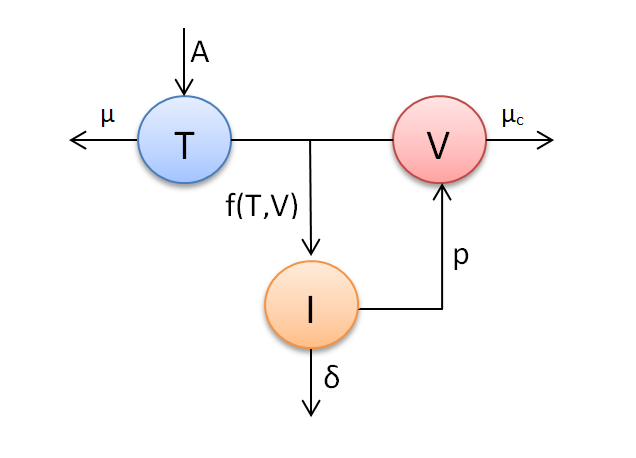
schematic representation of HIV dynamic.

We refer the reader to [4] and [5] for more general class on nonlinear incidence rates that take into account the saturation phenomenon.

We consider an age-structured HIV infection model with a very general nonlinear infection function

$\begin{equation} \label{A} \left \{ \begin{array}{lll} T'(t)=A- \mu T(t)-f(T(t),V(t)) \;\;\ t \geq 0,\\ i_t(t,a)+i_a(t,a)=-\delta(a) i(t,a), \\ V'(t)=\int_0^{\infty} p(a)i(t,a)da-\mu_cV(t), \end{array} \right. \end{equation}$

with the boundary and initial conditions

$\begin{equation} \begin{cases} i(t,0)=f(T(t),V(t)), \\ T(0)=T_0\geq 0, \quad V(0)=V_0 , \quad i(0,.)=i_0(.)\in L_{+}^{1}(\mathbb{R}^{+}). \end{cases} \end{equation}$

We denote by

$\Pi(a)=e^{-\int_0^a\delta(\theta)d\theta}, \qquad N=\int_0^{\infty}p(a)\Pi(a)da.$

The number $R_0$ represents the expected number of secondary infections produced by a single infected cell during its lifetime,

$R_0=\frac{N}{c}\dfrac{\partial f}{\partial V}(\frac{A}{d},0).$

The complete global stability analysis for the system (\ref{A}) has been studied in [4]. The system (\ref{A}) admits at most two equilibrium, from Theorem 3.1 and Theorem 5.2 in [4], we obtain the following result:

If $R_0 \leqslant 1$, the disease free equilibrium $E_0=(\frac{A}{\mu},0,0)$ is globally asymptotically stable.
If $R_0>1$, the positive infection equilibrium $E^{\ast}=(T^\ast,i^\ast,V^\ast)$ is globally asymptotically stable.

Numerical method

We consider the Beddington-Deangelis function $f$ defined by

$f(T, V)= \frac{\beta T V}{1+ \alpha_1 S+ \alpha_2 V}.$

In this case, the basic reproduction number ${\cal R}_0$ is given by

$R_0 = \displaystyle \frac{N}{\mu_c} \frac{A \beta }{\mu + \alpha_1}.$

Where $\pi(a)=\exp^{-\int_{0}^{a} \delta (s) ds}$ and $N=\int_{0}^{\infty} p(a) \pi(a) da$.

The numerical method to solve this system of equation is based on the upwind method for solving hyperbolic partial differential equation, (see [3]) called also the FTBS method (Forward-Time-Backward-Space), has first-order accuracy in both space and time. The CFL condition is necessary for the stability of numerical solutions. The ODEs are solving by explicit Euler method.

we use a grid with points $(x_j,t_n)$ defined by

$a_j=j\Delta a, \qquad j=0,...,N, \qquad t_n=n\Delta t, \qquad n=0,...,M.$

with age step $\Delta a$ and time step $\Delta t$. Denoting, respectively, by $T^n$, $i^n_j$ and $V^n$ the numerical approximation of $T(t_n)$, $i(t_n,a_j)$ and $V(t_n)$, moreover,

$\left( \frac{\partial i}{\partial t} \right)_n \simeq \frac{i^{n+1}_j-i^n_{j}}{\Delta t}, \qquad \left( \frac{\partial i}{\partial a} \right)_j \simeq \frac{i^n_j-u^n_{j-1}}{\Delta a}.$ we thus obtain the difference scheme of hyperbolic PDE

$i^{n+1}_j=(1-\lambda) i^n_j +\lambda i^n_{j-1}+ \Delta t \delta(a_j) i^n_j, \quad n=0,...,M-1, \text{ and } j=0,...,N.$

with $\lambda = \frac{\Delta t}{\Delta a}$. We fix the following values of parameters

$A_0=2, \qquad \mu=0.04\qquad \mu_c=0.5 \qquad \text{and} \qquad \delta =0.4,$

with the initial conditions

$T_0=20, \qquad V_0=5 \qquad \text{and} \qquad i_0(a)=4 e^{-0.3 a}.$

The functions $p$ is given by

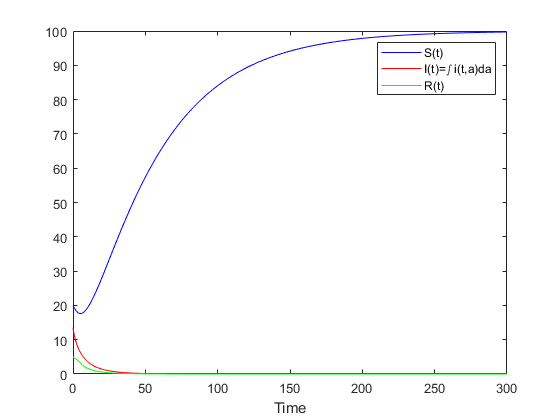
$\begin{equation*} p(a)=\left\{ \begin{array}{lll} 0, & \text{ if } a\leq \tau_1, \\ 0.4, & \text{ if } a> \tau_1, \end{array} \right. \end{equation*}$

We change the values of $\tau_1$ in order to have $R_0 \leq 1$ or to have $R_0 > 1$. If we choose $ \tau_1 = 3 $ then $ R_0 = 0.5417 < 1 $,

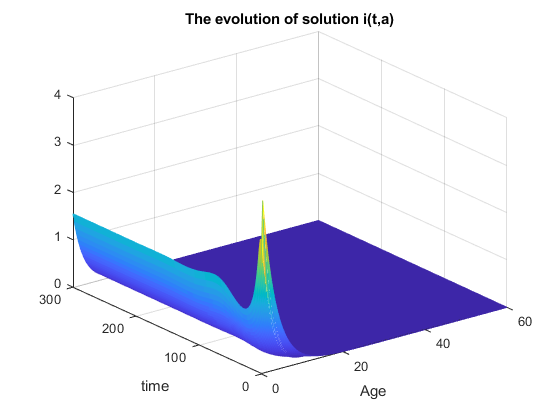
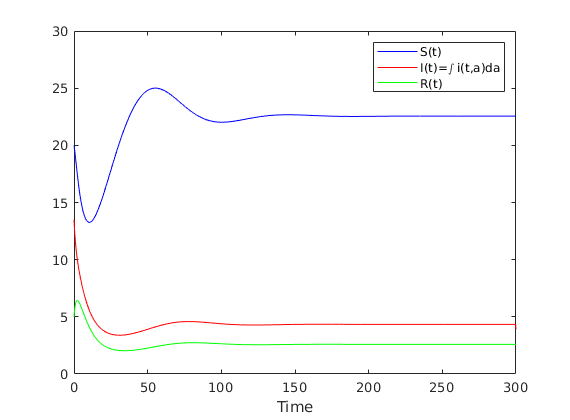
And if we choose $ \tau_1 = 0.5 $ then $ R_0 = 1.4216 > 1 $,

clear all,close all
a1=0;
a2=60;
Tf=300;
I0=@(t)4*exp(-0.3*t);
T0=20;
V0=5;
A0=2; mu=0.02; muc=0.4;
beta=0.1;
alpha1=0.1;
alpha2=0.2;
delta=0.4;
fct=@(x,y) (beta*x*y)/(1+alpha1*x+alpha2*y);
N=199;M=1200;
h=(a2-a1)/N;
k=Tf/M;
a=a1+(1:N)*h;
ap=[0,a];
t=0+(0:M)*k;
lambda=k/h;
C=eye(N);
A=(1-lambda)*C+lambda*diag(ones(1,N-1),-1);

The reproduction number $R_0$

R0=tauxR(N,h,a,delta,beta,muc,mu,A0,alpha1)


R0 =

    1.4216

T(1)=T0;
V(1)=V0;
U= I0(a(1:N))';  %% initial values
Up=[fct(T0,V0); U]; %% Initial value + Boundary condition
Uf=Up;

F=zeros(N,1);

UI=zeros(1,M);;

for j=1:M
    Uold=U;
      UI(j)=h*fct(T(j),V(j));
    for o=1:N
    UI(j)=UI(j)+h*Uold(o);
    end
    B=[lambda*fct(T(j),V(j)) ;zeros(N-1,1)];
    F=- delta*Uold ;
    U=A*Uold+B+k*F;
    val=feval(@int,Uold,N-1,h,a);
    T(j+1)=T(j)+k*(A0-mu*T(j)-fct(T(j),V(j)));
    V(j+1)=V(j)+k*(val - muc *V(j));
    Up=zeros(N+1,1);
    Up=[fct(T(j+1),V(j+1)); U];
    Uf=[Uf,Up];
end

 figure(1);
    [X , Y] = meshgrid( ap ,t);
 mesh (X , Y , Uf')
 title('The evolution of solution i(t,a)')
 xlabel('Age')
 ylabel('time')
 figure(2)
 plot(t,T','b',t,[UI UI(N+2)],'r',t,V','g')
 legend('S(t)','I(t)=\int i(t,a)da','R(t)')
 xlabel('Time')

References

[1] R. J. De Boer C. L. Althaus. Dynamics of immune escape during hiv/siv infection, PloS Comput. Biol, 2008.

[2] F. Brauer and C. Castillo-Chavez. Mathematical Models in Population Biology and Epidemiology Springer, New York, 2000.

[3] L. Edsberg. Introduction to Computation and Modeling for Differential Equations, 2nd Edition. Wiley, 288 Pages, 2016.

[4] M. N. Frioui S. E. Miri, T. M. Touaoula. Unified lyapunov functional for an age-structured virus model with very general nonlinear infection response. J. Appl. Math. Comput, pages 1–27, 2017.

[5] T. Kuniya J. Wang, R. Zhang.. Mathematical analysis for an age-structured hiv infection model with saturation infection rate, Elect. J. Diff. Eq, pages 1–19, 2015.

[6] A. S. Perelson P. W. Nelson. Mathematical analysis of delay differential equation models of hiv-1 infection. Math. Biosc, 179, pages 73–94, 2002.

Work Packages ≻ Models involving memory terms and hybrid PDE+ODE systems ≻

A numerical method for solving an age structured virus model

Introduction

Numerical method

References

Related Posts

Moving control strategy for memory-type equations

Simulation of Fractional Heat Equation

Optimal Control of the Fokker-Planck Equation with CasADi

Numerical simulation of nonlinear Population Dynamics Structuring by age and Spatial diffusion