Coupled transport equations and LQR control

Download Code

We consider the semilinear hyperbolic system

$\begin{cases} \partial_t y + \lambda \partial_x y = c_1 v + yv \quad & (x,t)\in (0,L)\times (0,T) \\ \partial_t v + \lambda \partial_x v = c_2 y + yv & (x,t)\in (0,L)\times (0,T) \\ y(0,t) = v(0,t) & t \in (0,T) \\ v(L,t) = u(t) & t \in (0,T) \\ y(x,0) = y^0(x) & x \in (0,L) \\ v(x,0) = v^0(x) & x \in (0,L), \end{cases}$

where $\lambda > 0$ and $u$ is the control. The stability and boundary stabilization of such 1D hyperbolic systems is studied in [1]. The aim of this tutorial is to semi-discretize in space this system of equations and design a stabilizing control by using the LQR method.

The above system linearized around $(y,v) = (0,0)$ has the form

$\begin{cases} \partial_t y + \lambda \partial_x y = c_1 v \quad & (x,t)\in (0,L)\times (0,T) \\ \partial_t v + \lambda \partial_x v = c_2 y & (x,t)\in (0,L)\times (0,T) \\ y(0,t) = v(0,t) & t \in (0,T) \\ v(L,t) = u(t) & t \in (0,T) \\ y(x,0) = y^0(x) & x \in (0,L) \\ v(x,0) = v^0(x) & x \in (0,L). \end{cases}$

We will first use the LQR method to design a stabilizing control for the semi-discretized linear system, and then this control will be applied to the semi-discretized semilinear system.

Space discretization

The intervall $(0,L)$ is divided in $n+1$ subintervals, of size $h_x := \frac{L}{n+1}$, by $n+2$ evenly spaced points $x_k = kh_x$. Hence, $x_0 = 0$ and $x_{n+1} = L$. We set $y_k(t) = y(x_k,t), \quad v_k(t) := v(x_k,t)$ and similarly for the inital conditions $y_k^0(t) = y^0(x_k)$ and $v_k^0(t) := v(x_k)$.

clear; clc;
L = 1; n = 30;
x = linspace(0, L, n+2);
hx = 1/(n+1);

The points where y and v are unknown are contained in x1 and x2 respectively, where x1 and x2 are defined below.

x1 = x(2:n+2);
x2 = x(1:n+1);

Finite differences for the space derivative give

$\partial_x y(x_k,t) \approx \begin{cases} \frac{y_1(t)}{h_x} - \frac{v_0(t)}{h_x} \quad & k=1\\ \frac{y_k(t)-y_{k-1}(t)}{h_x} \quad &\forall k \in \{2, \ldots, n+1 \} \end{cases}$

and

$\partial_x v(x_k,t) \approx \begin{cases} \frac{v_{k+1}(t)-v_{k}(t)}{h_x} &\forall k \in \{0, \ldots, n-1 \} \\ \frac{-v_n(t)}{h_x} + \frac{u(t)}{h_x} \quad &k=n. \end{cases}$

The sign of $\lambda$ in each equation must be taken into account to choose the approximation of $\partial_x y$ and $\partial_x v$.

Let $d = 2(n+1)$ represent the dimension of the state space for the semi-discretized systems. Defining the state variable $z \colon (0,T) \mapsto \mathbb{R}^d$ by

$z = \big(y_1, y_2, \ldots, y_{n+1}, v_0, v_1, \ldots, v_n \big)^\mathrm{T},$

the semilinear system writes as

$\begin{cases} \dot{z} = Az+ Bu + f(z,u) \qquad t \in (0,T)\\ z(0) = z_0, \end{cases}$

and the linearized system writes as

$\begin{cases} \dot{z} = Az+ Bu \qquad t \in (0,T)\\ z(0) = z^0. \end{cases}$

d = 2*(n+1);

We pick the initial condition

$z^0 := \big(y^0_1, y^0_2, \ldots, y^0_{n+1}, v^0_0, v^0_1, \ldots, v^0_n \big)^\mathrm{T}.$

y0 = sin(pi*x1)';
v0 = sin(pi*x2)';
z0 = zeros(d, 1); z0(1:n+1, 1) = y0; z0(n+2:d, 1) = v0;

We set values for $\lambda$, $c_1$ and $c_2$:

lambda = 1; c1 = 1; c2 = 1;

We consider the time parameters

T = 5;
nT = 70;
time = linspace(0, T, nT);

The matrix $A$ of size $d \times d$ is given by

$A = \begin{pmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{pmatrix},$

where $A_{11}, A_{12}, A_{21}, A_{22}$, of size $(n+1)\times(n+1)$, are defined by

$A_{11} = \begin{pmatrix} \frac{-\lambda}{h_x} & & & \\ \frac{\lambda}{h_x} & \ddots & & & \\ & \ddots & \ddots & \\ & & \frac{\lambda}{h_x} & \frac{-\lambda}{h_x} \end{pmatrix}, \quad A_{12} = \begin{pmatrix} \frac{\lambda}{h_x} & c_1 & & \\ & 0 & \ddots & \\ & & \ddots & c_1 \\ & & & 0 \\ \end{pmatrix}$

and

$A_{21} = \begin{pmatrix} 0 & & & \\ c_2 & \ddots & & \\ & \ddots & \ddots & \\ & & c_2 & 0 \end{pmatrix}, \quad A_{22}= \begin{pmatrix} \big(\frac{-\lambda}{h_x}+c_2\big) & \frac{\lambda}{h_x} & & \\ & \frac{-\lambda}{h_x} & \ddots & \\ & & \ddots & \frac{\lambda}{h_x} \\ & & & \frac{-\lambda}{h_x} \end{pmatrix}.$

They are constructed as follows.

A = zeros(d, d);
%% Lower and upper extradiagonals:
ext_down_1 = zeros(1,2*n+1); ext_down_1(1,1:n) = lambda/hx*ones(1,n);
ext_down_2 = c2*ones(1,n);
ext_up_1 = zeros(1,2*n+1); ext_up_1(1,(n+2):(2*n+1)) = lambda/hx*ones(1,n);
ext_up_2 = zeros(1, n+1); ext_up_2(1, 1) = lambda/hx;
ext_up_3 = c1*ones(1,n);
%% We assemple:
A = A - lambda/hx*eye(d); A(n+2, n+2) = A(n+2, n+2) + c2;
A = A + diag(ext_up_1,1) + diag(ext_up_2, n+1) + diag(ext_up_3,n+2);
A = A + diag(ext_down_1,-1) + diag(ext_down_2, -n-2);

The matrix $B$ is of size $d \times 1$ and is given by

$B = \begin{pmatrix} B_1 \\ B_2 \end{pmatrix},$

where $B_1, B_2$, of size $(n+1)\times 1$, are defined by

$B_1 = \begin{pmatrix} 0 \\ \vdots \\ 0 \\ c_1 \end{pmatrix}, \quad B_2 = \begin{pmatrix} 0 \\ \vdots \\ 0 \\ \frac{\lambda}{h_x} \end{pmatrix}.$

B= zeros(d, 1);
B(n+1, 1) = c1; B(d, 1) = lambda/hx;

The LQR method

We check that a LQR control can be computed for the semi-descretize linear system. To begin, we verify that $ (A,BB^\ast) $ is stabilizable (where $B^\ast$ denotes the transpose of $B$), meaning that $\text{rank}((sI-A) BB^\ast) = d$ for any eigenvalue $s$ of $A$ with a nonnegative real part.

disp('Stabilizability of (A, BB*):');
eA=eig(A);
not_stabilizable = 0;
for cpt=1:d
    if real(eA(cpt))>=0
        disp(cpt); disp(eA(cpt));

        M = zeros(d, 2*d);
        M(:, 1:d) = eA(cpt)*eye(d)-A;
        M(:, d+1:d*2) = B*(B');

        r = rank(M);
        if (r ~= d)
            not_stabilizable = not_stabilizable + 1;
        end
    end
end
if not_stabilizable == 0
    disp('stabilizable.');
else
    disp('not stabilizable.');
end

Stabilizability of (A, BB*):
    18

    0.3047

stabilizable.

Then, we verify that the eigenvalues of the Hamiltonian matrix

$H = \begin{pmatrix} A & -BB^* \\ -Q & -A^* \end{pmatrix}$

are not purely imzginary. Here, $Q$ is a matrix of size $d \times d$ to be chosen.

R = 1; Q = eye(d);
H = blkdiag(A, -A');
H(d+1: 2*d, 1:d) = -Q;
H(1:d, d+1: 2*d) = -B*(B');
eH = eig(H);
nb_imaginary_eig_val_hamiltonian = sum(real(eH) == 0);
disp('Number of eigenvalues of H on the imaginary axis:')
disp(nb_imaginary_eig_val_hamiltonian);

Number of eigenvalues of H on the imaginary axis:
     0

To finish, we verify that $(Q, A)$ is stabilizable, meaning that the rank of

$\begin{pmatrix} Q \\ sI-A \end{pmatrix}$

is equal to $d$, for any eigenvalue $s$ of $A$ with a nonnegative real part.

disp('Detectability of (Q, A):');
not_detectable = 0;
for cpt=1:d
    if real(eA(cpt))>=0
        disp(cpt); disp(eA(cpt));

        J = zeros(2*d, d);
        J(1:d, :) = Q;
        J(d+1:d*2, :) = eA(cpt)*eye(d)-A;

        r = rank(J);
        if (r ~= d)
            not_detectable = not_detectable + 1;
        end
    end
end
if not_detectable == 0
    disp('detectable.');
else
    disp('not detectable.');
end

Detectability of (Q, A):
    18

    0.3047

detectable.

The LQR control is given by the matlab routine care(), as the application $t \mapsto -Kz(t)$. The matrix $K$, of size $m \times d$ is an output of care(), where $m$ is the dimention of the input space and is equal to one.

[ricsol, cleig, K, report] = care(A, B, Q, R);
f_ctr = @(z) -K*z;

Unstable and stabilized system’s solutions

u = 0;

We compute the solution to the linear system with a control equal to zero:

F1 = @(t,z) A*z + B*u;
[t1, Z1] = ode45(F1, time, z0);

The corresponding solutions $y$ and $v$ are displayed:

[X,Y] = meshgrid(t1, x1);
figure; surf(X, Y, Z1(:, 1:n+1)');
xlabel('time'); ylabel('space'); title('Solution y for unstable linear system');

[X,Y] = meshgrid(t1, x2);
figure; surf(X, Y, Z1(:, n+2:2*(n+1))');
xlabel('time'); ylabel('space'); title('Solution v for unstable linear system');

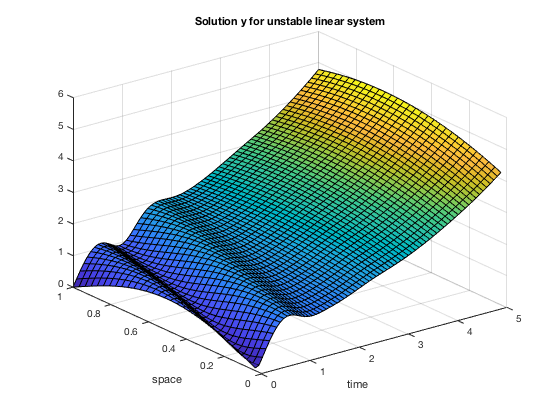
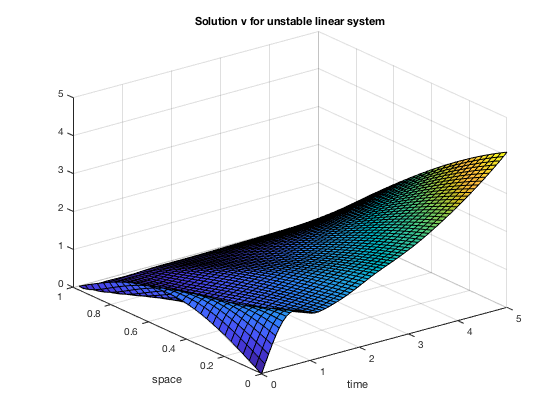
We compute the solution to the linear system with the feedback control:

F2 = @(t,z) A*z + B*f_ctr(z);
[t2, Z2] = ode45(F2, time, z0);

The corresponding solutions $y$ and $v$ are displayed:

[X,Y] = meshgrid(t2, x1);
figure; surf(X, Y, Z2(:, 1:n+1)');
xlabel('time'); ylabel('space'); title('Solution y for stabilized linear system');

[X,Y] = meshgrid(t2, x2);
figure; surf(X, Y, Z2(:, n+2:2*(n+1))');
xlabel('time'); ylabel('space'); title('Solution v for stabilized linear system');

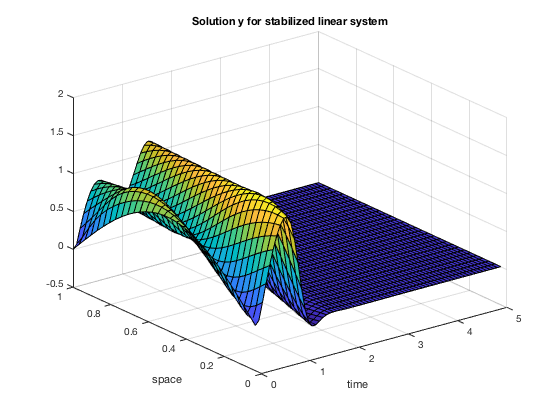
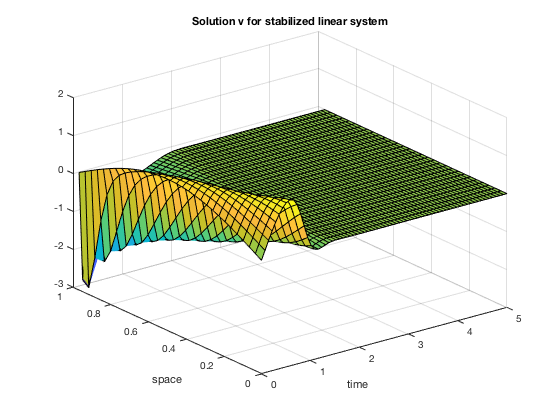
We compute the solution to the semilinear system with the same feedback control as the one found for the linear system:

F3 = @(t,z) A*z + B*f_ctr(z) + [z(1:n,1).*z(n+3:d,1);z(n+1, 1)*f_ctr(z);z(n+2, 1)^2 ; z(1:n,1).*z(n+3:d,1)];
[t3, Z3] = ode45(F3, time, z0);

The corresponding solutions $y$ and $v$ are displayed:

[X,Y] = meshgrid(t3, x1);
figure; surf(X, Y, Z3(:, 1:n+1)');
xlabel('time'); ylabel('space'); title('Solution y for stabilized semilinear system');

[X,Y] = meshgrid(t3, x2);
figure; surf(X, Y, Z3(:, n+2:2*(n+1))');
xlabel('time'); ylabel('space'); title('Solution v for stabilized semilinear system');

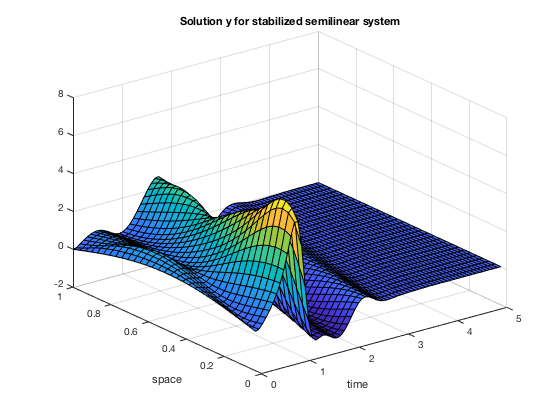
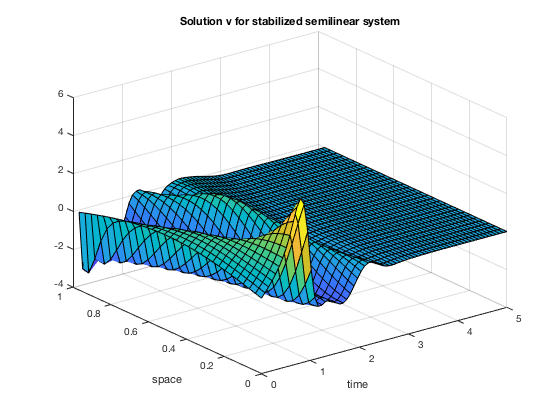
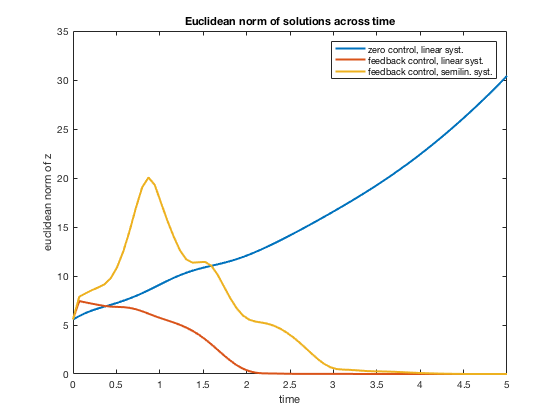
We compare the euclidean norm of the preceding solutions:

y1_norm = sum(abs(Z1(:, 1:n+1)).^2, 2);
y2_norm = sum(abs(Z2(:, 1:n+1)).^2, 2);
v1_norm = sum(abs(Z1(:, n+2:2*(n+1))).^2, 2);
v2_norm = sum(abs(Z2(:, n+2:2*(n+1))).^2, 2);
y3_norm = sum(abs(Z3(:, 1:n+1)).^2, 2);
v3_norm = sum(abs(Z3(:, n+2:2*(n+1))).^2, 2);
norm1 = (y1_norm + v1_norm).^(1/2);
norm2 = (y2_norm + v2_norm).^(1/2);
norm3 = (y3_norm + v3_norm).^(1/2);
figure;
plot(t1, norm1, 'lineWidth', 2);
hold on;
plot(t2, norm2, 'lineWidth', 2);
plot(t3, norm3, 'lineWidth', 2);
legend('zero control, linear syst.', 'feedback control, linear syst.', 'feedback control, semilin. syst.');
xlabel('time');
ylabel('euclidean norm of z');
title('Euclidean norm of solutions across time');

References

[1] Bastin G., J.-M. Coron, Stability and boundary stabilization of 1-D Hyperbolic systems. 2016.

Work Packages ≻ Models involving memory terms and hybrid PDE+ODE systems ≻

Coupled transport equations and LQR control

Space discretization

The LQR method

Unstable and stabilized system’s solutions

References

Related Posts

Moving control strategy for memory-type equations

Simulation of Fractional Heat Equation

Optimal Control of the Fokker-Planck Equation with CasADi

Numerical simulation of nonlinear Population Dynamics Structuring by age and Spatial diffusion