Reconstruction of traffic state using autonomous vehicles

A coupled PDE-ODE model

We consider the following hybrid PDE-ODE model

Above, (1a) and (1b) consists of a scalar conservation proposed by Lighthill-Whitham-Richards law modeling the evolution of vehicular traffic. (1c) and (1d) represent the trajectory of autonomous vehicles. $\rho$ stands for the density of cars and the flux function $f$ is defined by $f(\rho)=\rho v(\rho)$ with the average speed $v(\rho)=1-\rho$.

We assume that $\bar \rho_0$ is an unknown function and our goal is to find a time $T$ at which it is possible to reconstruct the true density $\rho$ between two autonomous vehicles based only on the measured local density of each autonomous vehicle.

We introduce the two following operators

• $S_t(\rho_0)(x)$ is the solution of (1a) at time $t$ and at the position $x$ with initial density $\rho_0$
• $\Gamma(\rho_0)=(\rho(\cdot,y_i(\cdot)\pm))_{i\in\{1,\cdots,M\}}$ where $(\rho,y_i)$ is the solution of (1) with initial data $\rho_0$.

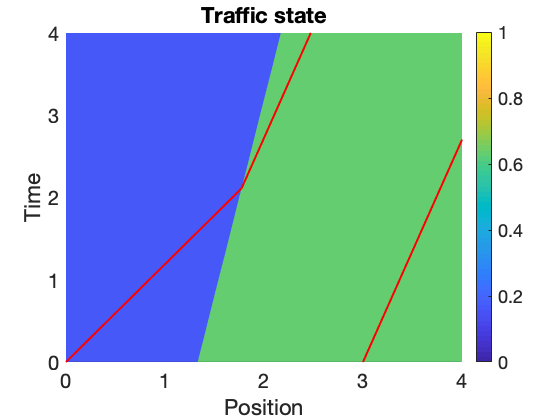
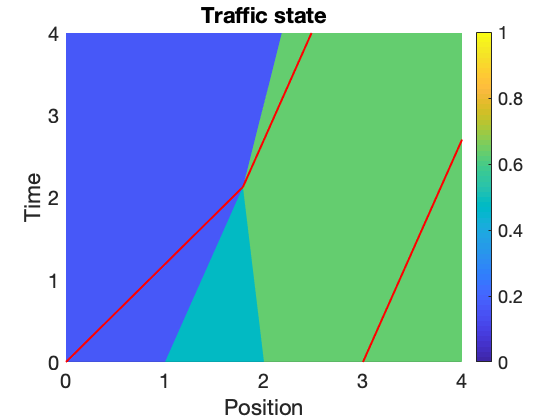
Figure 1.1 - $\rho_0(x)=0.16$ if $x<1.33$ and $\rho_0(x)=0.63$ if $x>1.33$ with two autonomous vehicles positioned at $y_0^1=0$ and $y_0^2=3$.						Figure 1.2 - $\rho_1(x)=0.16$ if $x<1$ and $\rho_0(x)=0.47$ if $1<x<2$ and $\rho_0(x)=0.63$ if $2<2$ with two connected vehicles positioned at $y_0^1=0$ and $y_0^2=3$

In Figure 1.1 and Figure 1.2, we construct two initial data $\rho_0$ and $\rho_1$ such that $\Gamma(\rho_0)=\Gamma(\rho_1)$ and for every $t < 2$ , for every $x\in[y_1(t),y_2(t)]$ , $S_T(\rho_0)(x) \neq S_T(\rho_1))(x)$. Thus, there isn’t backward uniqueness from the trajectory of autonomous vehicles.

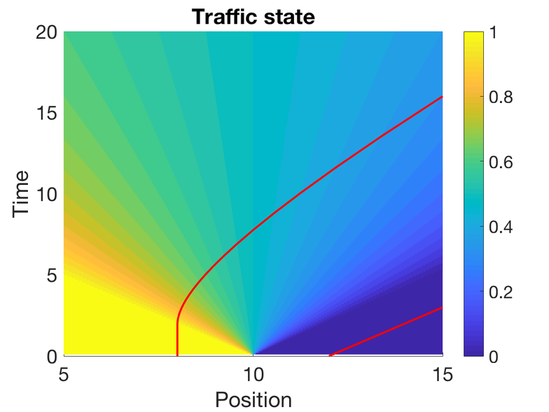Figure 1.3 $\rho_0(x)=1$ if $x<10$ and $\rho_0(x)=0$ if $x>10$ with two autonomous vehicles positioned at $x=8$ and $x=12$ respectively

In Figure Figure 1.3, we cannot reconstruct the traffic state at any time using data collected by the two autonomous vehicles. Some additional conditions on the set of initial densities will be require.

Theorem Let $\bar \rho_0 \in BV(R,[0,1])\cap L^1(R)$ and we assume that for every $x\in R$, $0<\rho_{\min}\leq \bar \rho_0(x) \leq \rho_{\max}$. For every $i\in \{1,\cdots,M-1\}$ there exists $T_i>0$ such that for every $\rho_0 \in \Gamma^{-1}(\Gamma(\bar \rho_0))$ and for almost every $x\in [y_i(T_i),y_{i+1}(T_i)]$ we have $S_{T_i}(\rho_0)(x)= S_{T_i}(\bar \rho_0)(x)$

The reconstruction time $T_i$ is obtained using the notion of generalized characteristics and $T_i$ has an implicit form.

Numerical simulations

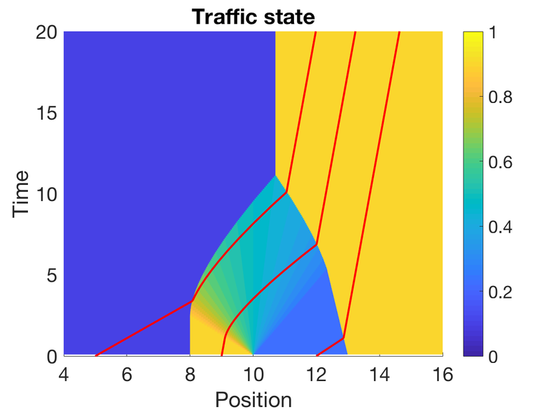
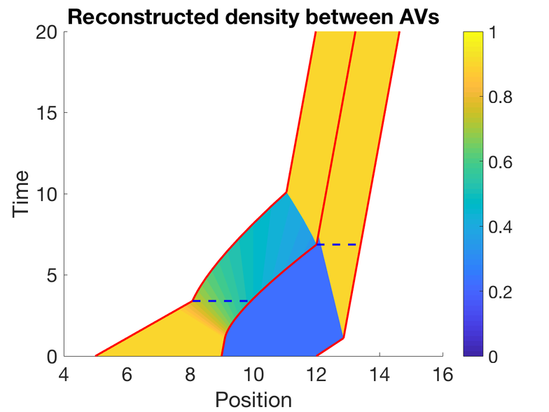
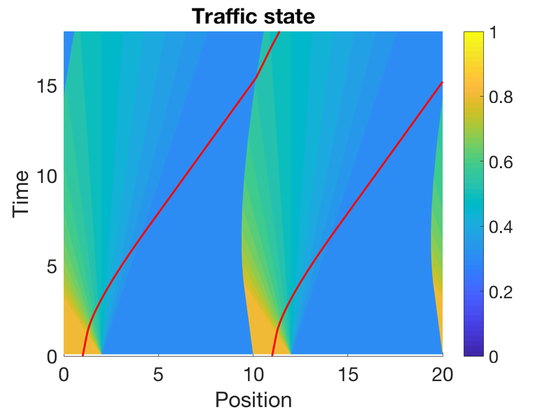
In Figure 2.1 and Figure 2.2, we consider the example of two shocks with a fan of rarefaction shocks between the two shocks. A total of three AVs, denoted by $AV_0$ , $AV_1$ and $AV_2$ , are used to reconstruct the traffic state resulting in two regions of reconstruction between $AV_0$ and $AV_1$ , and between $AV_1$ and $AV_2$ . Specifically, the initial density $\rho_0$ is defined as follows : $\rho_0(x) = 0.0938 $ for $ x\in (-\infty, 8] $, $\rho_0(x) = 0.9062$ for $x\in (8, 10]$, $\rho_0(x) = 0.2188$ for $x\in (10, 13]$ and $\rho_0(x) = 0.9062$ for $x\in (13, \infty)$. $AV_0$ , $AV_1$ , and $AV_2$ start at $x=5$ , $x=9$ , and $x=12$ , respectively. The resulting traffic state solved using wave front tracking over the first 20 seconds is shown in Figure 2.1, while the reconstructed state between the AVs is shown in Figure 2.2. The time at which the reconstruction becomes valid is $T_{0} = 6.87$ between $AV_0$ and $AV_1$, and $T_{1} = 3.39$ between $AV_1$ and $AV_2$.

Figure 2.1	Figure 2.2

In Figure 3.1 and Figure 3.2, one autonomous vehicle, denoted by $AV_0$ , is deployed on a ring. The initial density $\rho_0$ is a $10$-periodic function defined as follows: $\rho_0(x) = 0.8125$ for $x\in (0,2)$ , $\rho_0(x) = 0.3125$ for $x\in (2, 10)$ . Since $\rho$ and $y_0$ are also $10$ periodic functions, both trajectories plotted in red in Figure 3.2 are the ones of $AV_0$. The traffic state on the whole ring can be reconstructed after $T_{\max}=15.444$.

Figure 3.1	Figure 3.2

References

[1] T.Liard, B. Piccoli, R. Stern, D. Work. Traffic reconstruction using autonomous vehicles; submitted (2019)