Download Code
The time dependent transmission problem is as follows, where we consider a domain $\Omega \subset \mathbb{R}^2$ which is cut into two subdomains $\Omega_1 \cup \Omega_2 = \Omega$ with transmission conditions at the interface $\Gamma = \Omega_1 \cap \Omega_2$:
where $\textbf{n}_m$ is the outward normal to $\Omega_m$ for $m=1,2$.
The constants $\lambda_1$ and $\lambda_2$ describe the thermal conductivities of the materials on $\Omega_1$ and $\Omega_2$ respectively. $D_1$ and $D_2$ represent the thermal diffusivities of the materials and they are defined by
where $\rho_m$ represents the density and $c_{p_m}$ the heat capacity of the material placed in $\Omega_m$, $m=1,2$.
DISCRETIZATION
Let $u_I^{(1)}$ and $u_I^{(2)}$ correspond to the unknowns on $\Omega_1$ and $\Omega_2$ respectively and $u_{\Gamma}$ correspond to the unknows at the interface $\Gamma$, then the compact 2D finite difference (FD) formulation on equidistant meshes of (1) for the vector of unknowns
will be
for the mass matrices $M_m$, $M_{\Gamma \Gamma}^{(m)}$, $M_{I \Gamma}^{(m)}$, $M_{\Gamma I}^{(m)}$ and the stiffness matrices
for $m=1,2$.
Applying the implicit Euler method with time step $\Delta t$ to the system (3), we get for the vector of unknowns
DIRICHLET-NEUMANN ITERATION
We now employ a standard Dirichlet-Neumann iteration to solve the discrete system (4), getting in the $k$-th iteration the two equation systems
to be solved in succession. Here,
with some initial condition, here $u_{\Gamma}^{n+1,0} = u_{\Gamma}^{n}$. The iteration is terminated according to the standard criterion
where $\tau$ is a user defined tolerance.
IMPLEMENTATION
We consider here the thermal interaction between two different materials which physical properties are described by their thermal conductivities and diffusivities $\lambda_1$, $\lambda_2$ and $D_1$, $D_2$ respectively. Furthermore, we consider the non overlapping identical domains $\Omega_1 = [0,1] \times [0,1]$ and $\Omega_2 = [1,2] \times [0,1]$.
The initialization parameters look as follows:
Ns = 50; %% space discretization points in each dimension
dx = 1/(Ns+1); %% mesh size
tf = 0.5; t0=0; %% final time - initial time
Nt = 5; %% time discretization points
dt = (tf-t0)/Nt; %% stepsize
D1 = 0.5; %% thermal diffusivity of material on domain 1
D2 = 1; %% thermal diffusivity of material on domain 2
lambda1 = 0.3; %% thermal conductivity material on domain 1
lambda2 = 1; %% thermal conductivity material on domain 2
alpha1 = lambda1/D1;
alpha2 = lambda2/D2;
In addition to the parameters above, other objects need to be specified before starting the iterative procedure. The space grids both in $x$-direction and $y$-direction are given to later plot the numerical solution, also the initial conditions $u_m^0(x)$, $x \in \Omega_m$ and the mass and stiffness matrices coming from the space discretization:
space grid w.r.t component x
xplot = linspace(0,2,2*Ns+3);
%% space grid w.r.t component y
yplot = linspace(0,1,Ns+2);
%%
%% this functions gives the initial conditions w.r.t. domain 1 (U1_0), domain 2 (U2_0) and interface unknowns (UG_0).
[U1_0, U2_0, UG_0] = initial_conditions(Ns);
%%
%% this function calculates the discretization matrices using finite differences
[A1,A2,A1g,A2g,Ag1,Ag2,Agg1,Agg2,M1,M2,M1g,M2g,Mg1,Mg2,Mgg1,Mgg2] = compute_matrices(Ns,lambda1,lambda2,alpha1,alpha2);
Then, the iterative procedure takes place where the equations (4) and (5) are solved alternatively on $\Omega_1$ and $\Omega_2$ respectively until convergence is achieved at each time step. The implementation is specified below:
UG_old = UG_0; %% UG_0 is fixed over the Dirichlet-Neumann iteration while UG_old is being updated
figure(1)
%% gif('2D_FDM.gif','frame',figure(1))
for k=1:Nt %% time recursion
%% initial guess for the stopping criteria of the inner fixed point iteration
error = 10;
%% Dirichlet-Neumann iteration
while(error>1e-10)
%% solve problem on domain 1 using Dirichlet BC at the interface
U1 = solve_dirichlet(Ns,dt,U1_0,UG_0,A1,M1,A1g,M1g,UG_old);
%% solve problem on domain 2 using Neumann BC at the interface
[U2, UG_new] = solve_neumann(Ns,dt,U1_0,U2_0,UG_0,A2,M2,Ag2,Mg2,A2g,M2g,Agg1,Agg2,Mgg1,Mgg2,Ag1,Mg1,U1,UG_old);
%% calculate value for the stopping criteria (difference between two consecutive iterates at the interface)
error = norm(UG_old - UG_new);
%% update UG_old
UG_old = UG_new;
%%put together U1,U2 and UG_old for plotting
Uplot = zeros(Ns+2,2*Ns+3);
Uplot(2:end-1,2:Ns+1) = U1;
Uplot(2:end-1,Ns+2) = UG_old;
Uplot(2:end-1,Ns+3:end-1) = U2;
%% figure(1)
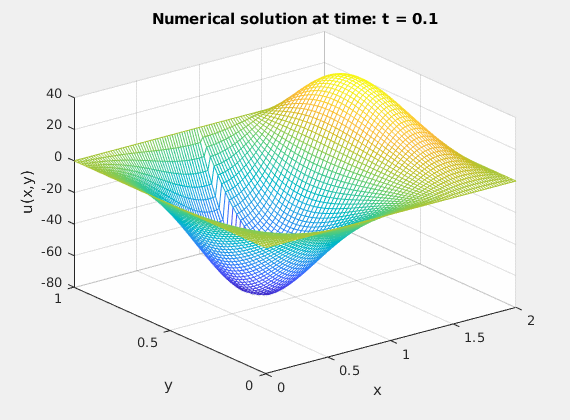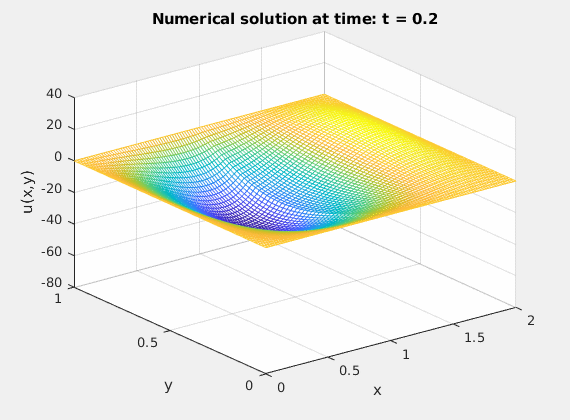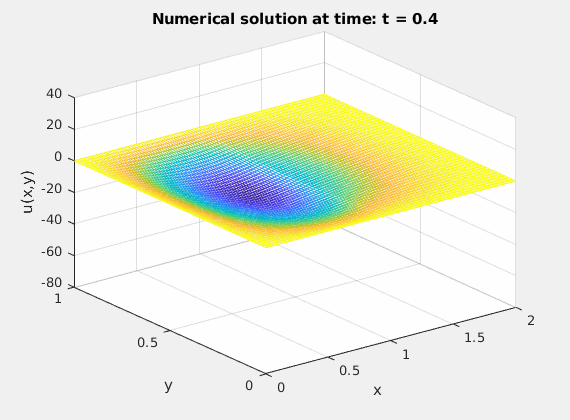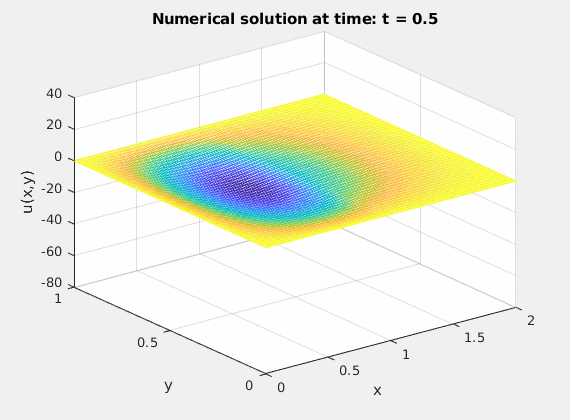
%% mesh(xplot,yplot,Uplot);
%% zlim([-80 40])
%% xlabel('x')
%% ylabel('y')
%% zlabel('u(x,y)')
%% title(['Numerical solution at time: t = ',num2str(k*dt)])
%% gif
%% pause(0.1)
end
%% update the initial values U1_0, U2_0 and UG_0 to start the next time
%% step
U1_0 = U1;
U2_0 = U2;
UG_0 = UG_old;
end