Download Code
We study the shape design problem through the minimization of the cost functional
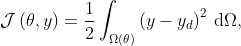
where 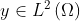 is the state variable,
is the state variable, 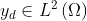 is a target function, and
is a target function, and 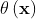 the normal displacement to a reference boundary,
the normal displacement to a reference boundary,
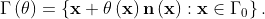
The problem is subject to the following elliptic PDE in the domain 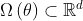 with Dirichlet boundary conditions on
with Dirichlet boundary conditions on 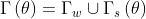 ,
,
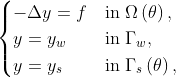
and 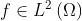 .
.
We consider the set of admissible domains whose measure is fixed,
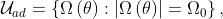
and aim at finding the optimal shape that minimizes the cost function. In order to do so, we use the steepest descent method with descent direction given by
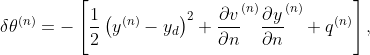
where  is solution of the adjoint problem
is solution of the adjoint problem
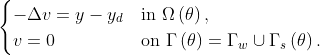
The normal displacement field is updated at every iteration,
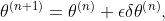
with  sufficiently small. The Lagrange multiplier is computed in order to ensure that the volume contraint is fulfilled, thus
sufficiently small. The Lagrange multiplier is computed in order to ensure that the volume contraint is fulfilled, thus
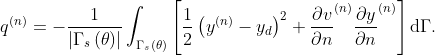
Mesh Motion Solver
The solutions to the primal and adjoint problems are commonly approximated by means of numerical methods, such as the finite element method (FEM) or the finite volume method (FVM). In order to apply these techniques, the domain under study must be tessellated with a mesh. Nevertheless, applying the displacement directly to the controlled boundary will deteriorate the surrounding elements after a few iterations and the computation will crash if the interior nodes of the domain are not reallocated. In order to avoid this, the domain can be re-meshed after a number of iterations. However, this can be very expensive as a completely new mesh must be generated. A commonly used alternative is to move the interior nodes of the mesh according to the displacements prescribed on the boundary. By doing this the number of elements and the nodes connectivities remain the same, only the mesh nodes positions are updated. The Solid Body Rotation Stress method and the Laplacian smoothing included in the OpenFOAM library have been used.
Linear Elasticity
Mesh motion can be achieved by treating the mesh as an elastic body and solving the equations of Linear Elasticity for solids with prescribed displacements on the domain boundary,
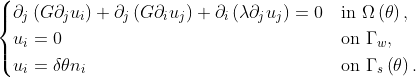
Solid Body Rotation (SBR) Stress
The Linear Elasticity model fails when dealing with rotating meshes. This can be mitigated by selecting the material properties in a proper manner,
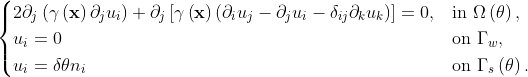
Laplacian Smoothing
A simple and widely used practice is to solve a Laplace equation with the prescribed displacements as boundary conditions,
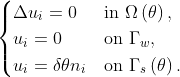
The behavior of the Laplacian smoothing can be improved by adding a non-uniform diffusivity term,
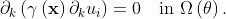
The diffusion field 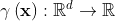 decreases with the distance to the controlled boundary. A common choice is to make it depend on the inverse of the distance as
decreases with the distance to the controlled boundary. A common choice is to make it depend on the inverse of the distance as
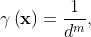
so that the nodes next to the deforming boundaries move with similar displacements as those on the boundary.
Getting Started
The solver must be compiled in the terminal. It is advisable to first clean previous compilations with
and then use
Dynamic Mesh
The mesh motion solver is specified in the dictionary constant/dynamicMeshDict.
- For the Laplacian solver:
dynamicFvMesh dynamicMotionSolverFvMesh;
motionSolverLibs ( "libfvMotionSolvers.so" );
solver displacementLaplacian;
displacementLaplacianCoeffs
{
//diffusivity uniform;
//diffusivity inversePointDistance (deformedWall);
diffusivity quadratic inversePointDistance (deformedWall);
}
motionSolver displacementSBRStress;
displacementSBRStressCoeffs
{
// diffusivity uniform;
// diffusivity directional (1 200 0);
// diffusivity motionDirectional (1 1000 0);
// diffusivity file motionDiffusivity;
// diffusivity quadratic inverseFaceDistance (deformedWall);
// diffusivity quadratic inverseDistance (deformedWall);
diffusivity quadratic inversePointDistance (deformedWall);
// diffusivity inversePointDistance (deformedWall);
}
Prerequisites
OpenFOAM C++ library must be installed in order to compile the code.
The OpenFOAM distribution provided by the OpenFOAM Foundation was used.
Running a Case
In order to run the solver move to the case folder poissonOptShapeFoamCase and type in the command line
./Allprepare
poissonOptShapeFoam
The shape optimization method described in the previous section has been tested with a simple example. The Poisson equation is posed in a two-dimensional circular domain with boundary
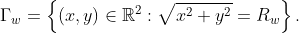
The reference geometry to be optimized is an inner hole with boundary given by
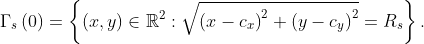
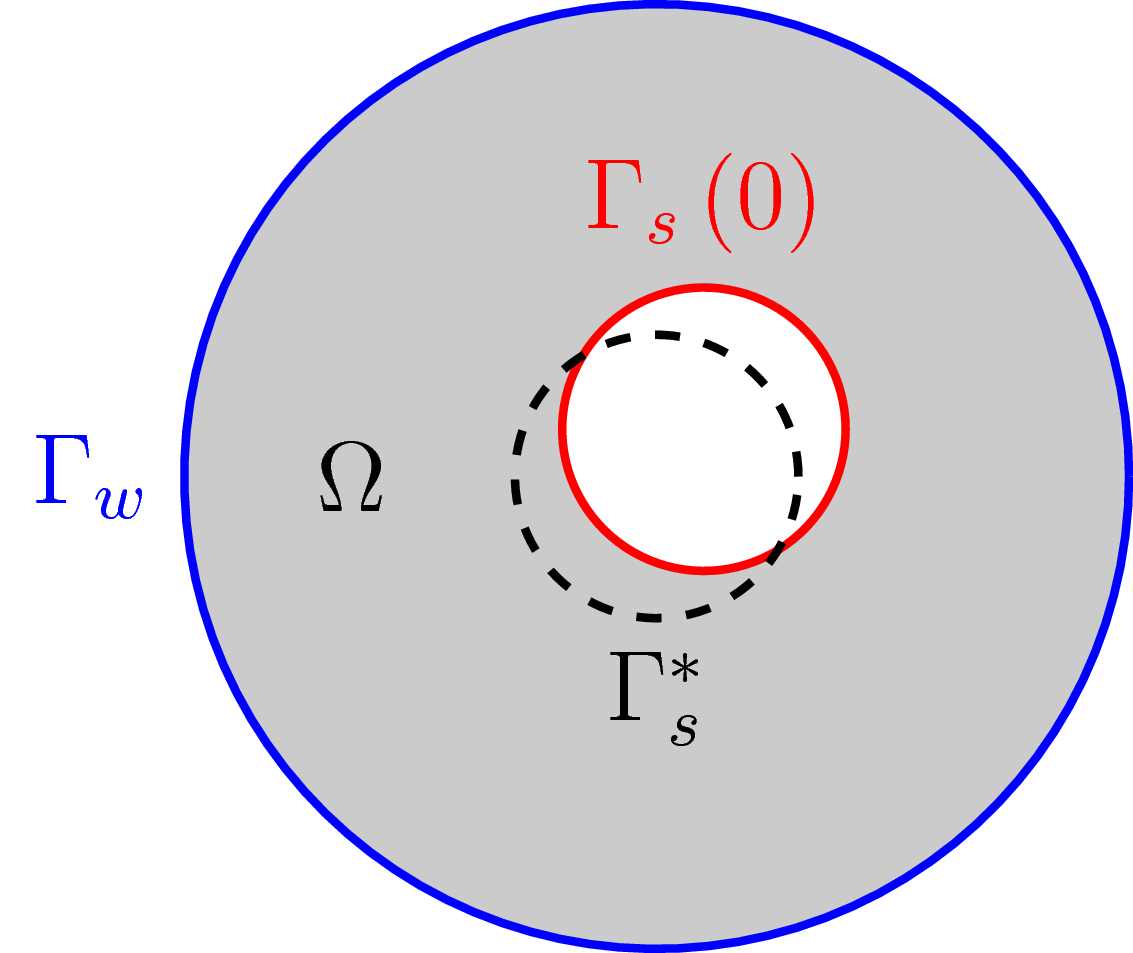
The target function 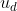 will be the analytical solution of the Poisson equation with the inner hole centered in the origin,
will be the analytical solution of the Poisson equation with the inner hole centered in the origin,
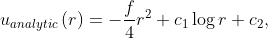
where the integration constants are obtained from the boundary conditions,
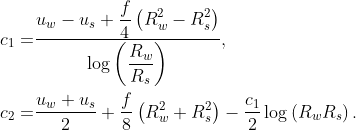
When the hole center is displaced from the origin, the target state must be extended in the region 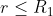 , thus
, thus
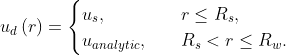
It is clear that for
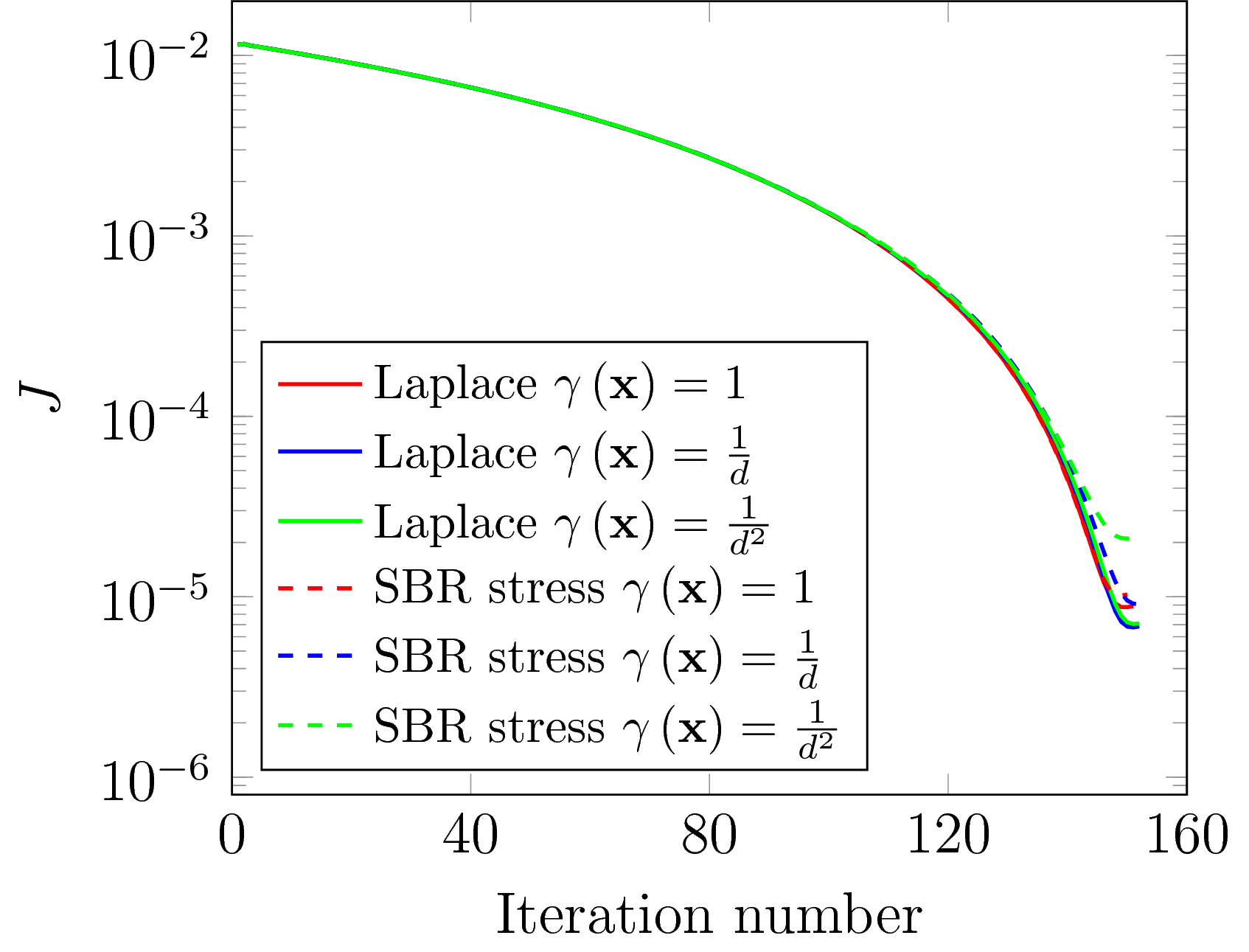
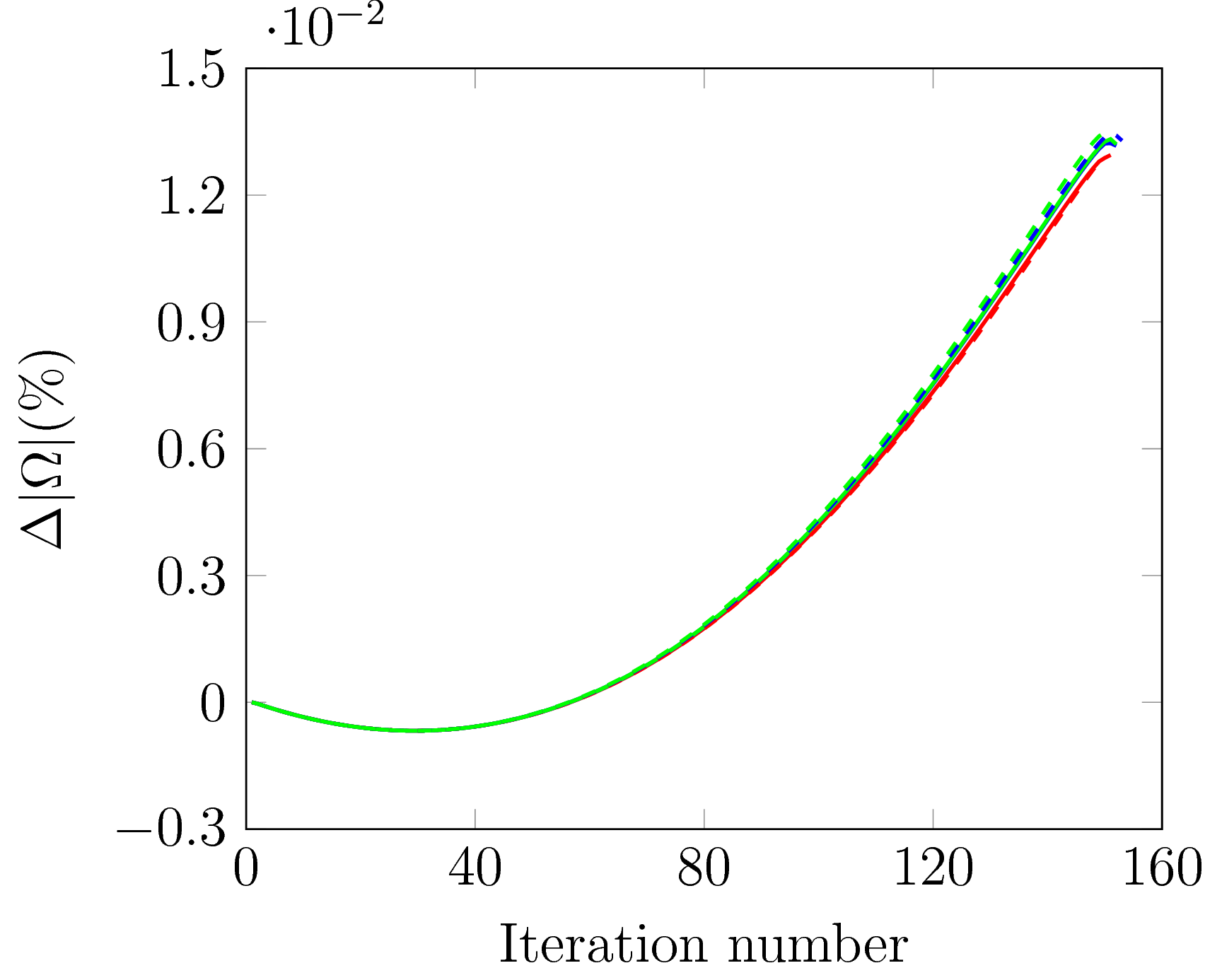
the cost function equals zero, thus it is an optimal solution. The steepest descent algorithm has been coded in the OpenFOAM solver poissonOptShapeFoam with  .
.

Warning
It might be needed to use
sed -i -e 's/\r$//' filename
and
in order to be able to execute
References
- O. Pironneau. Optimal shape design for elliptic systems. Springer Science & Business Media, 2012.
- J Simon. Diferenciación de problemas de contorno respecto del dominio. Technical report, Universidad de Sevilla, Facultad de Matemáticas, Departamento de Análisis Matemático, 1989.
- The OpenFOAM Foundation.
- Moving boundary problem based on calculated data, CFDonline, 2013.
Linear Elasticity mesh motion method:
- Andrew A. Johnson and Tayfun E. Tezduyar. Mesh update strategies in parallel finite element computations of flow problems with moving boundaries and interfaces. Computer methods in applied mechanics and engineering, 119(1-2):73–94, 1994.
- Thomas D. Economon, Francisco Palacios, and Juan J. Alonso. Unsteady continuous adjoint approach for aerodynamic design on dynamic meshes. AIAA Journal, 53(9):2437–2453, 2015.
- George S. Eleftheriou and Guillaume Pierrot. Rigid motion mesh morpher: A novel approach for mesh deformation. In OPT-i, An International Conference on Engineering and Applied Sciences Optimization, Kos, Greece, pages 4–6, 2014.
Solid Body Rotation (SBR) Stress method:
- Richard P. Dwight. Robust mesh deformation using the linear elasticity equations. In Computational fluid dynamics 2006, pages 401–406. Springer, 2009.
Laplacian Smoothing:
- Peter Hansbo. Generalized laplacian smoothing of unstructured grids. International Journal for Numerical Methods in Biomedical Engineering, 11(5):455–464, 1995.
- Rainald Löhner and Chi Yang. Improved ale mesh velocities for moving bodies. Communications in numerical methods in engineering, 12(10):599–608, 1996.
- Hrvoje Jasak and Zeljko Tukovic. Automatic mesh motion for the unstructured finite volume method. Transactions of FAMENA, 30(2):1–20, 2006.