Download Code
This is an OpenFOAM solver for the distributed control of the heat equation through the minimization problem
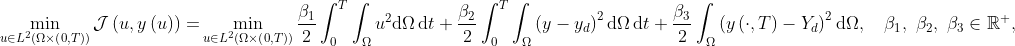
subject to the state equation
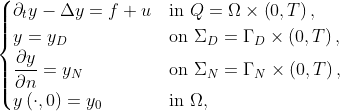
with 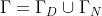 and
and 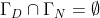 .
.
The cost functional gradient is
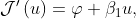
where 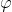 solves the adjoint problem
solves the adjoint problem
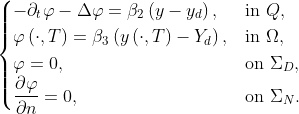
In the steepest descent method the cost gradient is used to update the control as
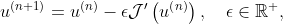
with  sufficiently small.
sufficiently small.
Getting Started
The solver must be compiled in the terminal. It is advisable to first clean previous compilations with
and then use
Prerequisites
OpenFOAM C++ library must be installed in order to compile the code.
The OpenFOAM distribution provided by the OpenFOAM Foundation was used.
Running a Case
In order to run the solver move to the case folder heatAdjoinFoamCase and type in the command line
./Allprepare
heatAdjointFoam
- The heatAdjointFoam solver has been tested in a square domain
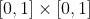 with zero Dirichlet boundary conditions,
with zero Dirichlet boundary conditions, 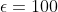 , and
, and 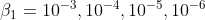 ,
, 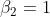 ,
, 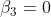 . The target function is
. The target function is 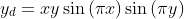 .
.



- The heatAdjointFoam solver has been tested in a square domain
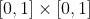 with zero Dirichlet boundary conditions,
with zero Dirichlet boundary conditions, 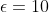 , and
, and 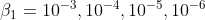 ,
, 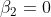 ,
,  . The target function is
. The target function is 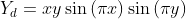 .
.



Warning
It might be needed to use
sed -i -e 's/\r$//' filename
and
in order to be able to execute