Download Code
In this work we solve the optimal control problem
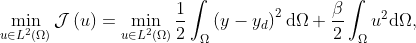
where 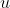 is the control variable,
is the control variable, 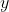 the state variable and
the state variable and 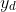 a target function. The minimization problem is subject to the elliptic partial differential equation
a target function. The minimization problem is subject to the elliptic partial differential equation
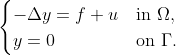
In order to use the conjugate gradient method, the state variable is separated in two terms as
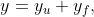
where 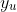 solves the state equation with zero Dirichlet boundary conditions,
solves the state equation with zero Dirichlet boundary conditions,
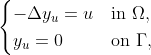
and 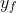 is the control-free solution to the state equation,
is the control-free solution to the state equation,
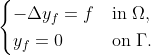
With the above separation of the state variable, the cost functional can be expressed as

We define a linear operator
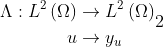
and its adjoint
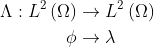
with 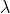 solution to
solution to
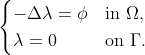
The directional derivative of the cost function then reads as
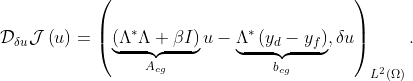
After having identified 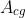 and
and 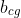 we can use the conjugate gradient method to reach the optimal control faster.
we can use the conjugate gradient method to reach the optimal control faster.
Getting Started
The solver must be compiled in the terminal. It is advisable to first clean previous compilations with
and then use
Prerequisites
OpenFOAM C++ library must be installed in order to compile the code.
The OpenFOAM distribution provided by the OpenFOAM Foundation was used.
Running a Case
In order to run the solver move to the case folder poissonCGAdjoinFoamCase and type in the command line
./Allprepare
poissonCGAdjointFoam
The poissonCGAdjointFoam solver has been tested in a square domain 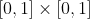 with zero Dirichlet boundary conditions and
with zero Dirichlet boundary conditions and 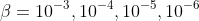 . The target function is
. The target function is 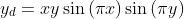 .
.
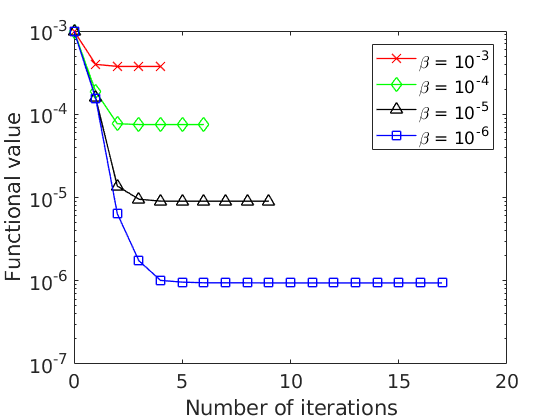
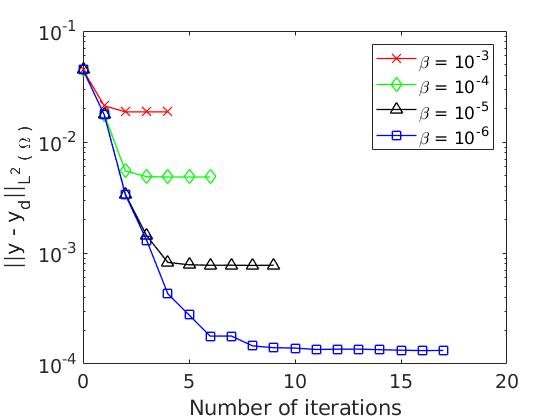
Warning
It might be needed to use
sed -i -e 's/\r$//' filename
and
in order to be able to execute
References
- F. Tröltzsch. Optimal control of partial differential equations: theory, methods, and applications. American Mathematical Soc., 2010.