Download Code
A natural application in the framework of shape optimization is the aerodynamic design of an airfoil. An object defined by a domain 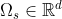 with boundary
with boundary 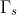 immersed in a fluid will experience a net force given by
immersed in a fluid will experience a net force given by

where  is the stress tensor,
is the stress tensor, 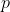 is the fluid pressure,
is the fluid pressure, 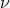 is the kinematic viscosity,
is the kinematic viscosity, 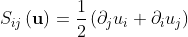 is the strain rate tensor, and
is the strain rate tensor, and 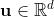 is the fluid velocity vector field.
is the fluid velocity vector field.
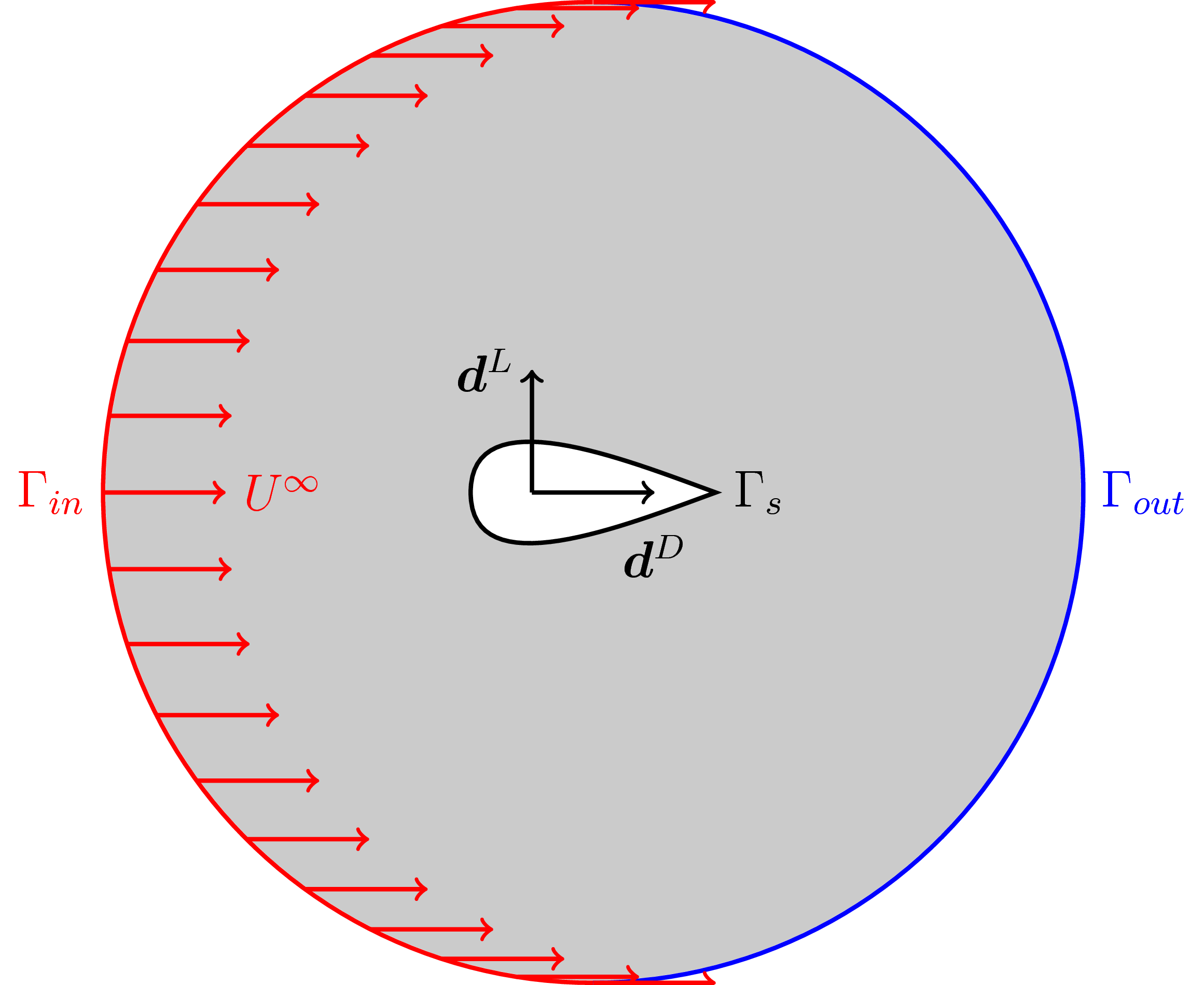
The force exerted by the fluid on the airfoil parallel to the fluid velocity at infinity is referred to as the drag force, whereas the force in perpendicular direction is often named the lift.


We look for the optimal shape in order to minimize the drag, as this force produces energy losses, and at the same time maximize the lift for a fixed airfoil volume. This can be expressed by means of the functional
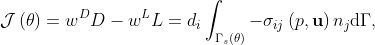
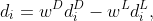
where 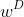 and
and 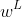 are weighting factors for drag and lift forces, respectively, and with
are weighting factors for drag and lift forces, respectively, and with 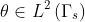 . The state variables are subject to a set of constraints in the fluid domain
. The state variables are subject to a set of constraints in the fluid domain 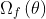 with boundary
with boundary 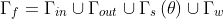 , namely the steady Navier-Stokes equations,
, namely the steady Navier-Stokes equations,
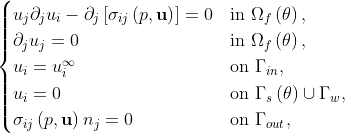
and to the volume constraint
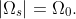
The adjoint problem reads as

The directional derivative of the functional is given by
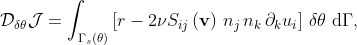
and the cost function descreases by choosing the normal displacement to the controlled boundary as
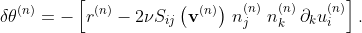
Hence,
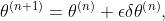
for a sufficiently small value of  .
.
The remaining Lagrange multiplier associated to the volume constraint is computed in order to ensure the volume conservation,
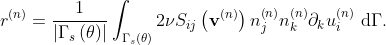
In summary, the shape optimization iteration is as follows:
- Solve the primal problem.
- Solve the adjoint problem with the previously computed state variables.
- Compute the Lagrange multiplier for the volume constraint.
- Compute the displacement field.
- Update the displacement field of the previous iteration.
- Perform the mesh motion.
Getting Started
The solver must be compiled in the terminal. It is advisable to first clean previous compilations with
and then use
Prerequisites
OpenFOAM C++ library must be installed in order to compile the code.
The OpenFOAM distribution provided by the OpenFOAM Foundation was used.
Running a Case
The above shape optimization process has been implemented in the open-source C++ library OpenFOAM. The already existing solver adjointShapeOptimizationFoam is a topological optimization routine that relies on a porosity variable and on the calculation of volume sensitivities to determine which regions of the domain must be blocked to the fluid passage in order to minimize a known functional. We have coded a new solver shapeOptimizationFoam that takes some ideas from the aforementioned one, but which performs a shape optimization iteration instead by computing shape sensitivities.
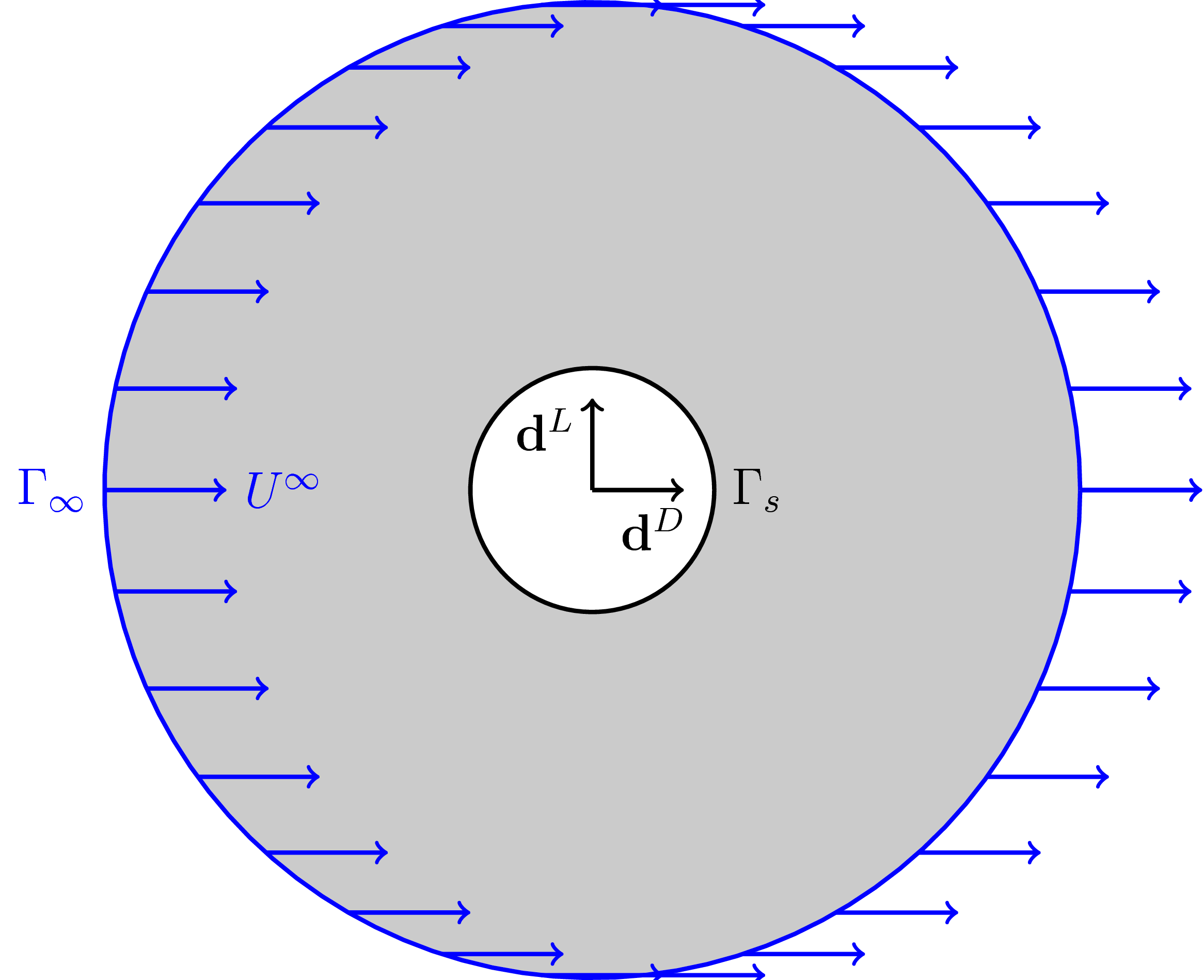
The solver has been tested in the minimization of the the cost function
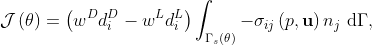
subject to

The adjoint problem reads as
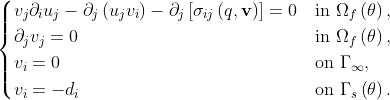
In order to run the solver move to the case folder shapeOptimizationFoamCase and type in the command line
./Allprepare
shapeOptimizationFoam
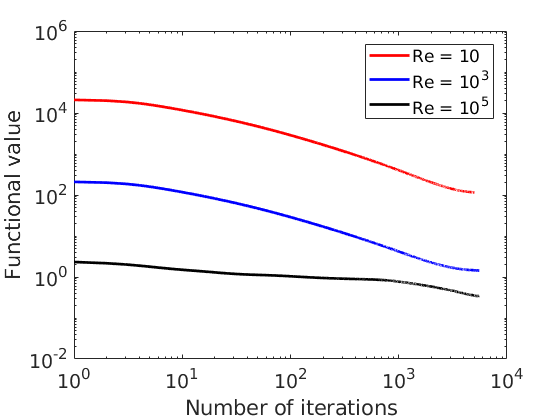
The solver has been run for three different Reynolds numbers and the cost functional value has been normalized with
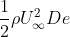
where 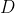 and
and  are the cylinder diameter and thickness, respectively.
are the cylinder diameter and thickness, respectively.
Warning
It might be needed to use
sed -i -e 's/\r$//' filename
and
in order to be able to execute
References
- Antony Jameson. Aerodynamic design via control theory. Journal of scientific computing, 3(3):233–260, 1988.
- Antony Jameson and Luigi Martinelli. Aerodynamic shape optimization techniques based on control theory. In Computational Mathematics Driven by Industrial Problems, pages 151–221. Springer, 2000.
- Antony Jameson and James Reuther. Control theory based airfoil design using the euler equations. In 5th Symposium on Multidisciplinary Analysis and Optimization, page 4272, 1994.
- Bijan Mohammadi and Olivier Pironneau. Mesh adaption and automatic differentiation in a cad-free framework for optimal shape design. International Journal for Numerical Methods in Fluids, 30(2):127–136, 1999.
- Bijan Mohammadi and Olivier Pironneau. Applied shape optimization for fluids. Oxford University Press, 2010.
- C. Othmer. A continuous adjoint formulation for the computation of topological and surface sensitivities of ducted flows. International Journal for Numerical Methods in Fluids, 58(8):861–877, 2008.
- C. Othmer, E. Papoutsis-Kiachagias, and K. Haliskos. CFD optimization via sensitivity-based shape morphing. In Proceedings of the 4th ANSA & μETA Internat. Conf., Thessaloniki, Greece, BETA CAE Systems SA, 2011.
- Carsten Othmer. Adjoint methods for car aerodynamics. Journal of Mathematics in Industry, 4(1):6, 2014.
- Carsten Othmer, Eugene de Villiers, and Henry Weller. Implementation of a continuous adjoint for topology optimization of ducted flows. In 18th AIAA Computational Fluid Dynamics Conference, page 3947, 2007.
- Carsten Othmer and Thorsten Grahs. Approaches to fluid dynamic optimization in the car development process. In International Conference on Evolutionary and Deterministic Methods for Design, Optimization and Control With Applications to Industrial and Societal Problems, 2005.
- Carsten Othmer, Thomas Kaminski, and Ralf Giering. Computation of topological sensitivities in fluid dynamics: cost function versatility. In ECCOMAS CFD 2006: Proceedings of the European Conference on Computational Fluid Dynamics, Egmond aan Zee, The Netherlands, September 5-8, 2006. Citeseer, 2006.
- Olivier Pironneau. Optimal shape design for elliptic systems. Springer Science & Business Media, 2012.
- James Reuther and Antony Jameson. Aerodynamic shape optimization of wing and wing-body configurations using control theory. In 33rd Aerospace Sciences Meeting and Exhibit, page 123, 1995.
- James Reuther, Antony Jameson, James Farmer, Luigi Martinelli, and David Saunders. Aerodynamic shape optimization of complex aircraft configurations via an adjoint formulation. In 34th Aerospace Sciences Meeting and Exhibit, page 94, 1996.
- James J Reuther, Antony Jameson, Juan J Alonso, Mark J Rimlinger, and David Saunders. Constrained multipoint aerodynamic shape optimization using an adjoint formulation and parallel computers, part 1. Journal of aircraft, 36(1):51–60, 1999.
- J. Simon. Diferenciación de problemas de contorno respecto del dominio. Technical report, Universidad de Sevilla, Facultad de Matemáticas, Departamento de Análisis Matemático, 1989.
- Orlando Soto and Rainald Löhner. On the computation of flow sensitivities from boundary integrals. AIAA paper, 112:2004, 2004.
- Orlando Soto, Rainald Löhner, and Chi Yang. An adjoint-based design methodology for CFD problems. International Journal of Numerical Methods for Heat & Fluid Flow, 14(6):734–759, 2004.
- Schumacher Thomas, Othmer Carsten, et al. Adjoint optimization for vehicle external aerodynamics. International Journal of Automotive Engineering, 7(1):1–7, 2016.
- Henk Kaarle Versteeg and Weeratunge Malalasekera. An introduction to computational fluid dynamics: the finite volume method. Pearson Education, 2007.
- F. Feppon, G. Allaire, F. Bordeu, J. Cortial, and C. Dapogny. Shape optimization of a coupled thermal fluid-structure problem in a level set mesh evolution framework, 2018.