Turnpike property for functionals involving $L^1$−norm

Download Code

Introduction

We introduce the following notation: $L^2=L^2\left(\Omega\right)$, $L^2_T=L^2\left(\Omega\times \left(0,T\right)\right)$,

$$\begin{eqnarray*} \langle u,v \rangle&=&\int_{\Omega}^{} u(x)v(x) \ dx;\\ \langle u,v \rangle_T^2&=&\int_{0}^{T} \int_{\Omega}^{} u(x,t)v(x,t) \ dx \ dt \end{eqnarray*}$$

and the correspondent norms $\norm{\cdot}=\langle \cdot,\cdot\rangle$ and $\norm{\cdot}_T=\langle \cdot,\cdot\rangle_T$. Moreover, we define the norms

$$\begin{eqnarray*} \norm{v}_{1}&=&\int_{\Omega}^{} \abs{v(x)} \ dx;\\ \norm{v}_{1,T}&=&\int_{0}^{T} \int_{\Omega}^{} \abs{v(x,t)} \ dx \ dt. \end{eqnarray*}$$

We want to study the following optimal control problem:

$$\begin{equation*} \left(\mathcal{P}\right) \ \ \ \ \ \ \ \hat{u}\in argmin_{u\in L^2_T} \left\{J\left(u\right)=\alpha_c \norm{u}_{1,T} + \frac{\beta}{2}\norm{u}^2_{T}+\alpha_s \norm{Lu}_{1,T} + \frac{\gamma}{2}\norm{Lu-z}_{T}^2\right\}, \end{equation*}$$

where $L: \ L^2_T \to L^2_T$ is defined by

$$\begin{eqnarray*} Lu&=&y \end{eqnarray*}$$

and $y$ is the solution of the PDE given by

$$\begin{equation*} \begin{cases} y'+Ay=Bu & \left(\Omega \times \left(0,T\right)\right)\\ y=0 & \left(\partial\Omega\times \left(0,T\right)\right)\\ y(0)=0 & \left(\Omega\right). \end{cases} \end{equation*}$$

Notice that, by integration by parts, $ L^*\mu=B^\ast p $, where $\varphi$ is solution of the adjoint equation:

$$\begin{equation*} \begin{cases} -p'+A^* p =\mu & \left(\Omega \times \left(0,T\right)\right)\\ p=0 & \left(\partial\Omega\times \left(0,T\right)\right)\\ p(T)=0 & \left(\Omega\right). \end{cases} \end{equation*}$$

Sparse control: $\alpha_c>0$ ($\alpha_s=0$)

The stationary problem

$$\begin{equation*} \left(\mathcal{S}\mathcal{P}_c\right) \ \ \ \ \ \ \ \bar{u}\in argmin_{u\in L^2} \left\{J_s\left(u\right)=\alpha_c \norm{u}_{1} + \frac{\beta}{2}\norm{u}^2+ \frac{\gamma}{2}\norm{y-z}^2: \ \ \ Ay=Bu \right\}. \end{equation*}$$

Optimality conditions

$$\begin{equation*} \begin{cases} A\bar{y}=B \ shrink(-B^*\bar{p},\frac{\alpha_c}{\beta}) & \left(\Omega\right)\\ A^*\bar{p}=\gamma\left(\bar{y}-z\right) & \left(\Omega\right)\\ \bar{y}=0, \ \bar{p}=0 & \left(\partial\Omega\right). \end{cases} \end{equation*}$$

Numerical algorithm

In order to compute a numerical solution of problem

$$\left(\mathcal{S}\mathcal{P}_c\right)$$

after a discretization by finite differences, we use a prox-prox splitting: first write the state as $y=A^{-1}Bu$, then

• Proximal-point step:
$$ \begin{equation*} \begin{split} \tilde{u}_{k} & =argmin_{u\in L^2} \left\{\frac{\beta}{2}\norm{u}^2 + \frac{\gamma}{2}\norm{A^{-1}Bu-z}^2+ \frac{1}{2\lambda_k}\norm{u-u_k}^2\right\}\\ & = \left[\left(\beta+\frac{1}{\lambda_k}\right)I+\gamma B^*A^{-*}A^{-1}B\right]^{-1}\left(\frac{1}{\lambda_k}u_k+\gamma B^*A^{-*}z\right). \end{split} \end{equation*} $$
• Proximal-point step:
$$ \begin{equation*} \begin{split} u_{k+1}& =argmin_{u\in L^2} \left\{\alpha_c \norm{u}_{1,T} + \frac{1}{2\lambda_k}\norm{u-\tilde{u}_k}_{T}^2\right\}\\ & = shrink(\tilde{u}_k,\alpha_c \lambda_k). \end{split} \end{equation*} $$

Remark: Notice that, when $\alpha_s=0$, the solution of $\left(\mathcal{P}^c_s\right)$ is simply given by

$$\bar{u}=\gamma \left[\beta I+\gamma B^*A^{-*}A^{-1}B\right]^{-1}B^*A^{-*}z.$$

Evolutionary problem

$$\begin{equation*} \left(\mathcal{P}_c\right) \ \ \ \ \ \ \ \hat{u}\in argmin_{u\in L^2_T} \left\{J\left(u\right)=\alpha_c \norm{u}_{1,T} + \frac{\beta}{2}\norm{u}^2_{T} + \frac{\gamma}{2}\norm{Lu-z}_{T}^2\right\}. \end{equation*}$$

Optimality conditions

Define the classical Lagrangian

$$\begin{equation*} \begin{split} \mathcal{L}\left(u,y,p\right)&=J\left(u\right)+\langle p, Bu-y'-Ay\rangle_T. \end{split} \end{equation*}$$

By integration by parts, we have

$$\begin{equation*} \begin{split} \mathcal{L}\left(u,y,p\right)&=\alpha_c \norm{u}_{1,T} + \frac{\beta}{2}\norm{u}^2_{T}+ \frac{\gamma}{2}\norm{y-z}_{T}^2 + \langle B^*p, u\rangle_T \\ & \quad + \langle p'-A^*p,y\rangle_T + \langle p(0),y(0)\rangle - \langle p(T),y(T)\rangle. \end{split} \end{equation*}$$

Deriving with respect to the three variables $\left(u,y,p\right)$, we obtain the optimality system:

$$\begin{equation*} \begin{cases} \hat{y}'+A\hat{y}=B\hat{u} & \left(\Omega \times \left(0,T\right)\right)\\ -\hat{p}'+A^*\hat{p}=\gamma\left(y-z\right) & \left(\Omega \times \left(0,T\right)\right)\\ \hat{y}=0, \ \hat{p}=0 & \left(\partial\Omega\times \left(0,T\right)\right)\\ \hat{y}(0)=0, \ \hat{p}(T)=0 & \left(\Omega\right), \end{cases} \end{equation*}$$

where the relation between the optimal control and the dual state is given by

$$\begin{equation*} 0\in \alpha_c \ \partial \norm{\cdot}_{1,T} \left(\hat{u}\right) + \beta \hat{u} + B^*\hat{p}. \end{equation*}$$

The latter is equivalent to

$$\begin{equation*} \begin{split} \hat{u}&=\left(\beta I+\alpha_c \ \partial \norm{\cdot}_{1,T} \right)^{-1}\left(-B^*\hat{p}\right)\\ &=argmin_{v\in L^2_T} \left\{ \alpha_c \norm{v}_{1,T}+\frac{1}{2\beta}\norm{v+B^*\hat{p}}_T^2 \right\}\\ &=shrink(-B^*\hat{p},\frac{\alpha_c}{\beta}), \end{split} \end{equation*}$$

where the operator of $soft-shrinkage$ is defined by

$$\begin{equation*} shrink(t,\alpha)= \begin{cases} t+\alpha & (t<-\alpha)\\ 0 & (-\alpha\leq t \leq \alpha)\\ t-\alpha & (t>\alpha). \end{cases} \end{equation*}$$

Finally,

$$\begin{equation*} \begin{cases} \hat{y}'+A\hat{y}=B \ shrink(-B^*\hat{p},\frac{\alpha_c}{\beta})& \left(\Omega \times \left(0,T\right)\right)\\ -\hat{p}'+A^*\hat{p}=\gamma\left(y-z\right) & \left(\Omega \times \left(0,T\right)\right)\\ \hat{y}=0, \ \hat{p}=0 & \left(\partial\Omega\times \left(0,T\right)\right)\\ \hat{y}(0)=0, \ \hat{p}(T)=0 & \left(\Omega\right). \end{cases} \end{equation*}$$

Numerical algorithm

In order to compute a numerical solution of problem $\left(\mathcal{P}_c\right)$, after a discretization by finite differences, we use a grad-prox splitting:

• Gradient step:
$$ \begin{equation*} \begin{split} \tilde{u}_{k} & = u_k-\lambda_k \nabla_u \left[\frac{\beta}{2}\norm{u}^2_{T} + \frac{\gamma}{2}\norm{Lu-z}_{T}^2 \right]\left(u_k\right) \\ & = u_k-\lambda_k \left[\beta u_k+\gamma L^*\left(Lu_k-z\right)\right]\\ & = u_k - \lambda_k\left[\beta u_k+\gamma B^*p_k\right], \end{split} \end{equation*} $$ where $$ \begin{equation*} \begin{cases} y_k'+Ay_k=Bu_k & \left(\Omega \times \left(0,T\right)\right)\\ y_k=0 & \left(\partial\Omega\times \left(0,T\right)\right)\\ y_k(0)=0 & \left(\Omega\right) \end{cases} \end{equation*} $$ and $$ \begin{equation*} \begin{cases} -p_k'+A^* p_k =y_k-z & \left(\Omega \times \left(0,T\right)\right)\\ p_k=0 & \left(\partial\Omega\times \left(0,T\right)\right)\\ p_k(T)=0 & \left(\Omega\right). \end{cases} \end{equation*} $$
• Proximal-point step:
$$ \begin{equation*} \begin{split} u_{k+1}& =argmin_{u\in L^2_T} \left\{\alpha_c \norm{u}_{1,T} + \frac{1}{2\lambda_k}\norm{u-\tilde{u}_k}_{T}^2\right\}\\ & = shrink(\tilde{u}_k,\alpha_c \lambda_k). \end{split} \end{equation*} $$

Remarks: Another possibility is to include the term $\frac{\beta}{2}\norm{u}^2_{T}$ in the proximal step. Notice that, for

$$f(u)=\frac{\beta}{2}\norm{u}^2_{T} + \frac{\gamma}{2}\norm{Lu-z}_{T}^2,$$

then $\nabla f$ is Lipschitz continuous. Indeed, for $u_i\in L^2_T$ ($i=1,2$), then

$$\nabla f (u_i)=\beta u_i+\gamma B^{*}p_i,$$

where

$$\begin{equation*} \begin{cases} y_i'+Ay_i=Bu_i & \left(\Omega \times \left(0,T\right)\right)\\ y_i=0 & \left(\partial\Omega\times \left(0,T\right)\right)\\ y_i(0)=0 & \left(\Omega\right) \end{cases} \end{equation*}$$

and

$$\begin{equation*} \begin{cases} -p_i'+A^* p_i=y_i-z & \left(\Omega \times \left(0,T\right)\right)\\ p_i=0 & \left(\partial\Omega\times \left(0,T\right)\right)\\ p_i(T)=0 & \left(\Omega\right). \end{cases} \end{equation*}$$

By linearity $\delta y=y_2-y_1$ and $\delta p=p_2-p_1$ solve the same equations with right-hand-sides $B(u_2-u_1)$ and $\delta y$, respectively. Then

$$\begin{equation*} \begin{split} \norm{\nabla f(u_2)-\nabla f(u_1)}&\leq \beta\norm{u_2-u_1}_T + \gamma \norm{B^*}\norm{\delta p}_T\\ &\leq \beta\norm{u_2-u_1}_T + \gamma \ C_{adj} \norm{B} \norm{\delta y}_T\\ & \leq \beta\norm{u_2-u_1}_T + \gamma \ C_{adj} C \ \norm{B} \norm{B(u_2-u_1)}_T\\ & \leq L \norm{u_2-u_1}_T, \end{split} \end{equation*}$$

where we defined

$$L=\beta+\gamma \ C_{adj} C \ \norm{B}^2.$$

In order the prox-grad method to converge, the restriction on the step size is given by

$$0<\lambda \leq \lambda_k \leq \Lambda <\frac{2}{L}.$$

Sparse state: $\alpha_s>0$ ($\alpha_c=0$)

$$\begin{equation*} \left(\mathcal{P}_s\right) \ \ \ \ \ \ \ \hat{u}\in argmin_{u\in L^2_T} \left\{J\left(u\right)=\frac{\beta}{2}\norm{u}^2_{T}+\alpha_s \norm{Lu}_{1,T} + \frac{\gamma}{2}\norm{Lu-z}_{T}^2\right\}. \end{equation*}$$

The stationary problem

$$\begin{equation*} \left(\mathcal{S}\mathcal{P}_s\right) \ \ \ \ \ \ \ \bar{u}\in argmin_{u\in L^2} \left\{J_s\left(u\right)=\alpha_c \norm{u}_{1} + \frac{\beta}{2}\norm{u}^2+ \frac{\gamma}{2}\norm{y-z}^2: \ \ \ Ay=Bu \right\}. \end{equation*}$$

Optimality conditions

$$\begin{equation*} \begin{cases} A\bar{y}=-\frac{1}{\beta}BB^*\hat{p} & \left(\Omega \times \left(0,T\right)\right)\\ \hat{y}=shrink(A^*\hat{p}+\gamma z,\frac{\alpha_s}{\gamma}) & \left(\Omega \times \left(0,T\right)\right)\\ \bar{y}=0, \ \bar{p}=0 & \left(\partial\Omega\times \left(0,T\right)\right). \end{cases} \end{equation*}$$

Finally, we obtain a single equation in the dual variable $p$:

$$\begin{equation*} \begin{cases} A \ shrink(A^*\bar{p}+\gamma z,\frac{\alpha_s}{\gamma})=-\frac{1}{\beta}BB^*\bar{p} & \left(\Omega \times \left(0,T\right)\right)\\ \bar{p}=0 & \left(\partial\Omega\times \left(0,T\right)\right). \end{cases} \end{equation*}$$

Numerical algorithm

In order to compute a numerical solution of problem $\left(\mathcal{P}_s\right)$, after a discretization by finite differences, we use a prox-prox splitting on the Augmented Energy: first write the state as $y=A^{-1}Bu$, then

• Proximal-point step:
$$ \begin{equation*} \begin{split} u_{k+1} & =argmin_{u\in L^2} \left\{\frac{\beta}{2}\norm{u}^2 + \frac{\gamma}{2}\norm{A^{-1}Bu-z}^2+\frac{\delta}{2\lambda_k}\norm{A^{-1}Bu-y_k}^2 +\frac{1}{2\lambda_k}\norm{u-u_k}^2\right\}\\ & = \left[\left(\beta+\frac{1}{\lambda_k}\right)I+\left(\gamma+\frac{\delta}{\lambda_k}\right) B^*A^{-*}A^{-1}B\right]^{-1}\left[\frac{1}{\lambda_k}u_k+ B^*A^{-*}\left(\gamma z+\frac{\delta}{\lambda_k}y_k\right)\right]. \end{split} \end{equation*} $$
• Proximal-point step:
$$ \begin{equation*} \begin{split} y_{k+1}& =argmin_{y\in L^2} \left\{ \alpha_s \norm{y}_{1} + \frac{\delta}{2\lambda_k}\norm{y-A^{-1}Bu_{k+1}}^2+\frac{1}{2\lambda_k}\norm{y-y_k}_{T}^2\right\}\\ & = shrink(\tilde{y}_k,\tilde{\lambda}_k), \end{split} \end{equation*} $$ where we defined $$ \begin{eqnarray*} \tilde{y}_k & = & \frac{y_k+\delta A^{-1}B u_{k+1}}{1+\delta};\\ \tilde{\lambda}_k & = & \frac{\alpha_s \lambda_k}{1+\delta}. \end{eqnarray*} $$

Remark: Notice that again, when $\alpha_s=0$, the solution of $\left(\mathcal{P}_s\right)$ is simply given by

$$\bar{u}=\gamma \left[\beta I+\gamma B^*A^{-*}A^{-1}B\right]^{-1}B^*A^{-*}z.$$

Evolutionary problem

Optimality conditions

Define the classical Lagrangian

$$\begin{equation*} \begin{split} \mathcal{L}\left(u,y,p\right)&=J\left(u\right)+\langle p, Bu-y'-Ay\rangle_T. \end{split} \end{equation*}$$

By integration by parts, we have

$$\begin{equation*} \begin{split} \mathcal{L}\left(u,y,p\right)&=\frac{\beta}{2}\norm{u}^2_{T}+\alpha_s \norm{y}_{1,T} + \frac{\gamma}{2}\norm{y-z}_{T}^2 + \langle B^*p, u\rangle_T \\ & \quad + \langle p'-A^*p,y\rangle_T + \langle p(0),y(0)\rangle - \langle p(T),y(T)\rangle. \end{split} \end{equation*}$$

Deriving with respect to the three variables $\left(u,y,p\right)$, we obtain the optimality system:

$$\begin{equation*} \begin{cases} \hat{y}'+A\hat{y}=B\hat{u} & \left(\Omega \times \left(0,T\right)\right)\\ -\hat{p}'+A^*\hat{p}\in\gamma\left(\hat{y}-z\right)+\alpha_s \ \partial \norm{\cdot}_{1,T} \left(\hat{y}\right) & \left(\Omega \times \left(0,T\right)\right)\\ \hat{y}=0, \ \hat{p}=0 & \left(\partial\Omega\times \left(0,T\right)\right)\\ \hat{y}(0)=0, \ \hat{p}(T)=0 & \left(\Omega\right), \end{cases} \end{equation*}$$

where the relation between the optimal control and the dual state is given by

$$\begin{equation*} \hat{u} = -\frac{1}{\beta}B^*\hat{p}. \end{equation*}$$

The adjoint equation is equivalent to

$$\begin{equation*} \begin{split} \hat{y}&=\left(\gamma I+\alpha_s \ \partial \norm{\cdot}_{1,T} \right)^{-1}\left(-\hat{p}'+A^*\hat{p}+\gamma z\right)\\ &=shrink(-\hat{p}'+A^*\hat{p}+\gamma z,\frac{\alpha_s}{\gamma}). \end{split} \end{equation*}$$

Finally,

$$\begin{equation*} \begin{cases} \hat{y}'+A\hat{y}=-\frac{1}{\beta}B B^*\hat{p} & \left(\Omega \times \left(0,T\right)\right)\\ \hat{y}=shrink(-\hat{p}'+A^*\hat{p}+\gamma z,\frac{\alpha_s}{\gamma}) & \left(\Omega \times \left(0,T\right)\right)\\ \hat{y}=0, \ \hat{p}=0 & \left(\partial\Omega\times \left(0,T\right)\right)\\ \hat{y}(0)=0, \ \hat{p}(T)=0 & \left(\Omega\right), \end{cases} \end{equation*}$$

Numerical algorithm

In order to compute a numerical solution of problem $\left(\mathcal{P}_s\right)$, after a discretization by finite differences, we use a grad-prox splitting on the following Augmented Energy:

$$\begin{equation*} \mathcal{L}_{\lambda}\left(u,y\right)=\frac{\beta}{2}\norm{u}^2_{T}+\alpha_s \norm{y}_{1,T}+ \frac{\gamma}{2}\norm{Lu-z}_{T}^2+\frac{\delta}{2\lambda}\norm{Lu-y}_{T}^2. \end{equation*}$$

Then,

• Gradient step:
$$ \begin{equation*} \begin{split} u_{k+1} & = u_k-\lambda_k \nabla_u \left[\frac{\beta}{2}\norm{u}^2_{T}+ \frac{\gamma}{2}\norm{Lu-z}_{T}^2+\frac{\delta}{2\lambda}\norm{Lu-y}_{T}^2 \right]\left(u_k\right) \\ & = u_k-\lambda_k \left[\beta u_k+\gamma L^*\left(Lu_k-z\right)+\frac{\delta}{\lambda_k}L^*\left(Lu_k-y_k\right)\right]\\ & = \left(1-\beta\lambda_k\right)u_k - B^*p_k, \end{split} \end{equation*} $$ where $$ \begin{equation*} \begin{cases} y_{u_k}'+Ay_{u_k}=Bu_k & \left(\Omega \times \left(0,T\right)\right)\\ y_{u_k}=0 & \left(\partial\Omega\times \left(0,T\right)\right)\\ y_{u_k}(0)=0 & \left(\Omega\right) \end{cases} \end{equation*} $$ and $$ \begin{equation*} \begin{cases} -p_k'+A^* p_k =\left(\gamma \lambda_k + \delta\right)y_{u_k}-\gamma \lambda_k z - \delta y_k & \left(\Omega \times \left(0,T\right)\right)\\ p_k=0 & \left(\partial\Omega\times \left(0,T\right)\right)\\ p_k(T)=0 & \left(\Omega\right). \end{cases} \end{equation*} $$
• Proximal-point step:
$$ \begin{equation*} \begin{split} y_{k+1}& =argmin_{y\in L^2_T} \left\{\alpha_s \norm{y}_{1,T} + \frac{\delta}{2\lambda_k}\norm{y-Lu_{k+1}}_T^2+\frac{1}{2\lambda_k}\norm{y-y_k}_{T}^2\right\}\\ & = shrink(\tilde{y}_k,\tilde{\lambda}_k), \end{split} \end{equation*} $$ where we defined $$ \begin{eqnarray*} \tilde{y}_k & = & \frac{y_k+\delta L u_{k+1}}{1+\delta};\\ \tilde{\lambda}_k & = & \frac{\alpha_s \lambda_k}{1+\delta}. \end{eqnarray*} $$
Remark: Another possibility is to consider $$ \begin{equation*} \mathcal{L}_{\lambda}\left(u,y\right)=\frac{\beta}{2}\norm{u}^2_{T}+\alpha_s \norm{y}_{1,T}+ \frac{\gamma}{2}\norm{y-z}_{T}^2+\frac{\delta}{2\lambda}\norm{Lu-y}_{T}^2. \end{equation*} $$

Computational experiments

In the following, we present the setting for the numerical experiments.
• Spacial domain: $\Omega=\left(0,1\right)$;
• Time interval: $\left[0,T\right]$, with $T=1$;
• Weight-parameters: $\alpha_c=[0, 0.01]$, $\alpha_s=[0, 0.65]$, $\beta=0.0001$ and $\gamma=1$;
• Trajectory target: $$z(x)=\mathcal{I}_{\left[x_a,x_b\right]},$$ where $x_a=1.7/3$, $x_b=3.5/4$;
• Control operator: for $x_1=1/7$ and $x_2=4/5$, $$B=\mathcal{I}_{\left[x_1,x_2\right]};$$
• $A$ is the finite difference discretization of $-\Delta$;
• Numerical grid: $N_x=300$ in space, $N_t=100$ in time.

Stationary solutions

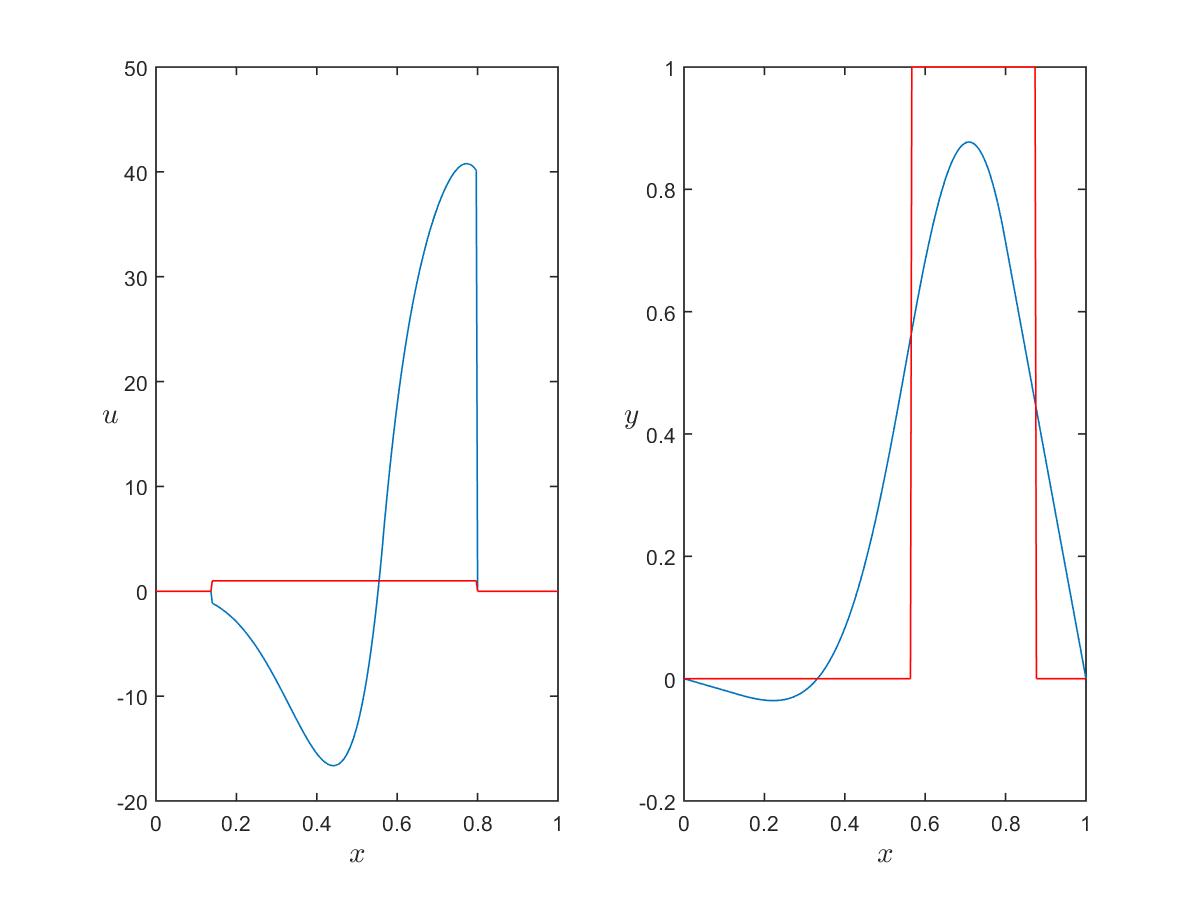Figure 1: $\alpha_c=\alpha_s=0$. 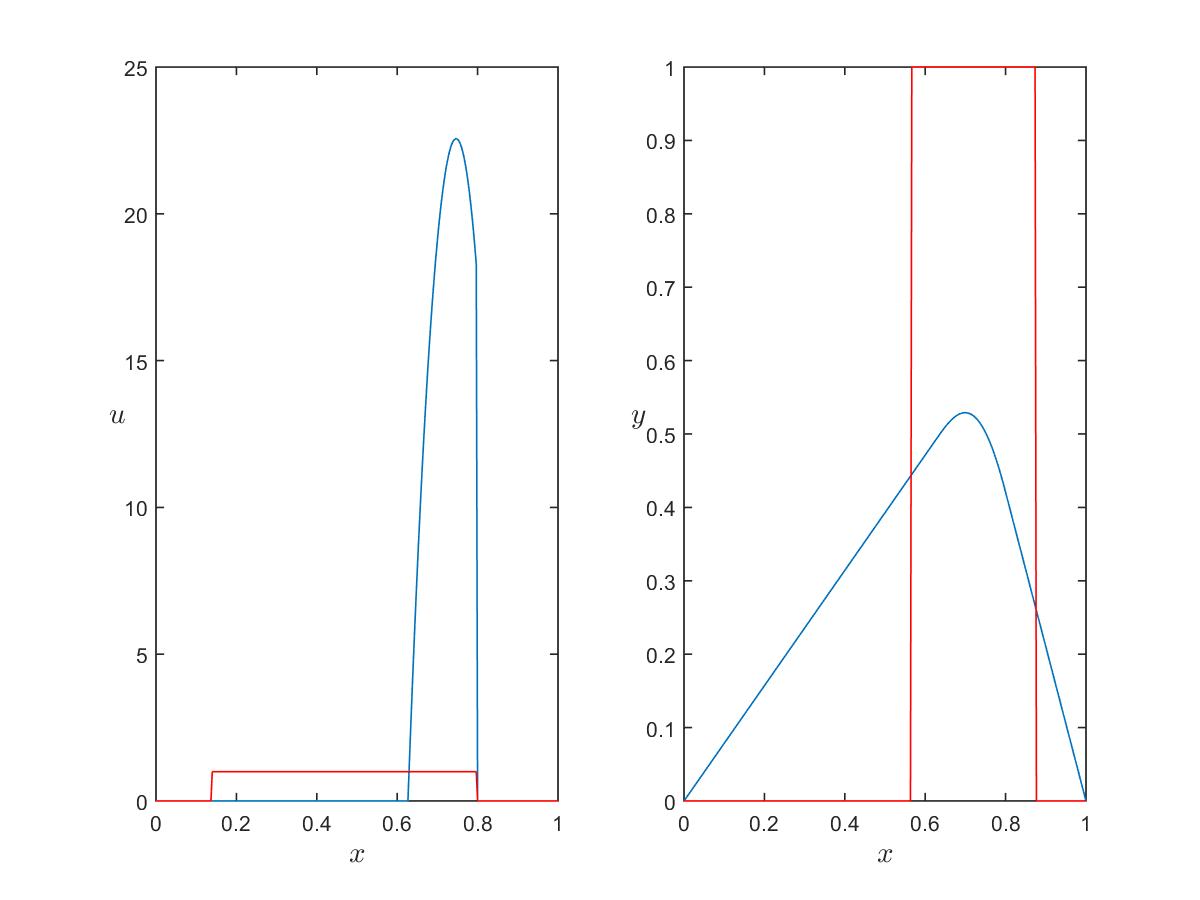Figure 2: $\alpha_c=0.01$, $\alpha_s=0$. 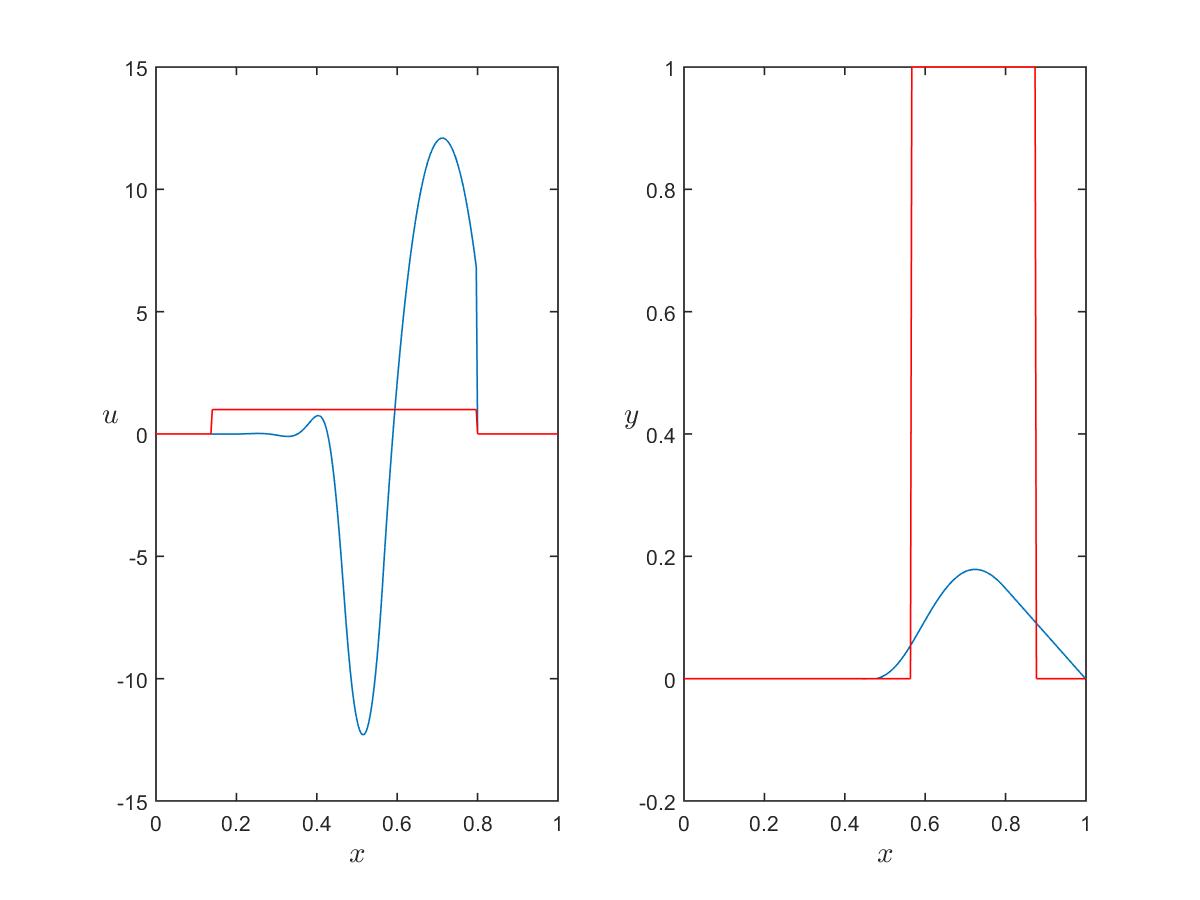Figure 3: $\alpha_c=0$, $\alpha_s=0.65$.

Evolutionary problem

Optimal control

Figure 4a: Optimal control for $\alpha_c=\alpha_s=0$. In red, the controllable subdomain; in blue, the stationary optimal controls. 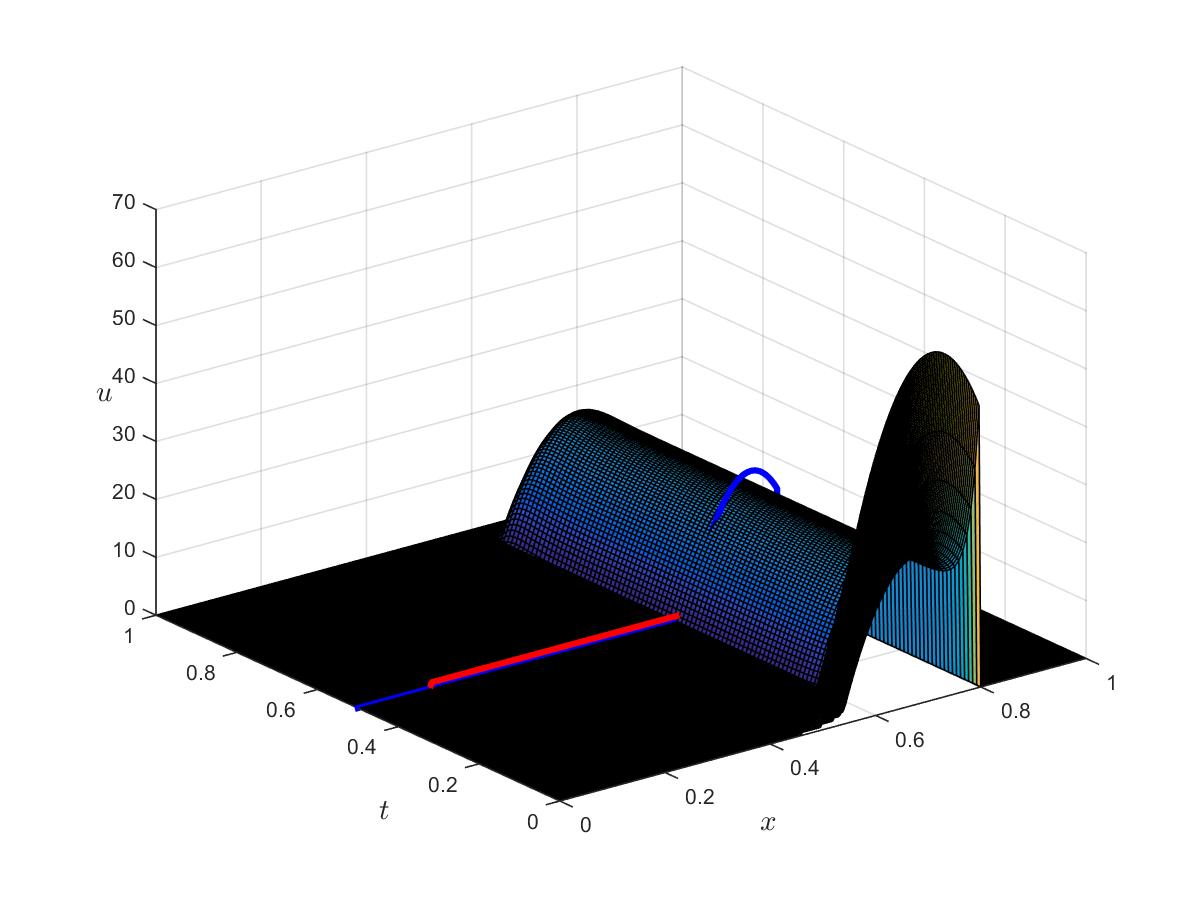Figure 4b: Optimal control for $\alpha_c=0.01$, $\alpha_s=0$. In red, the controllable subdomain; in blue, the stationary optimal controls. Figure 4c: Optimal control for $\alpha_c=0$, $\alpha_s=0.65$. In red, the controllable subdomain; in blue, the stationary optimal controls.

Optimal state

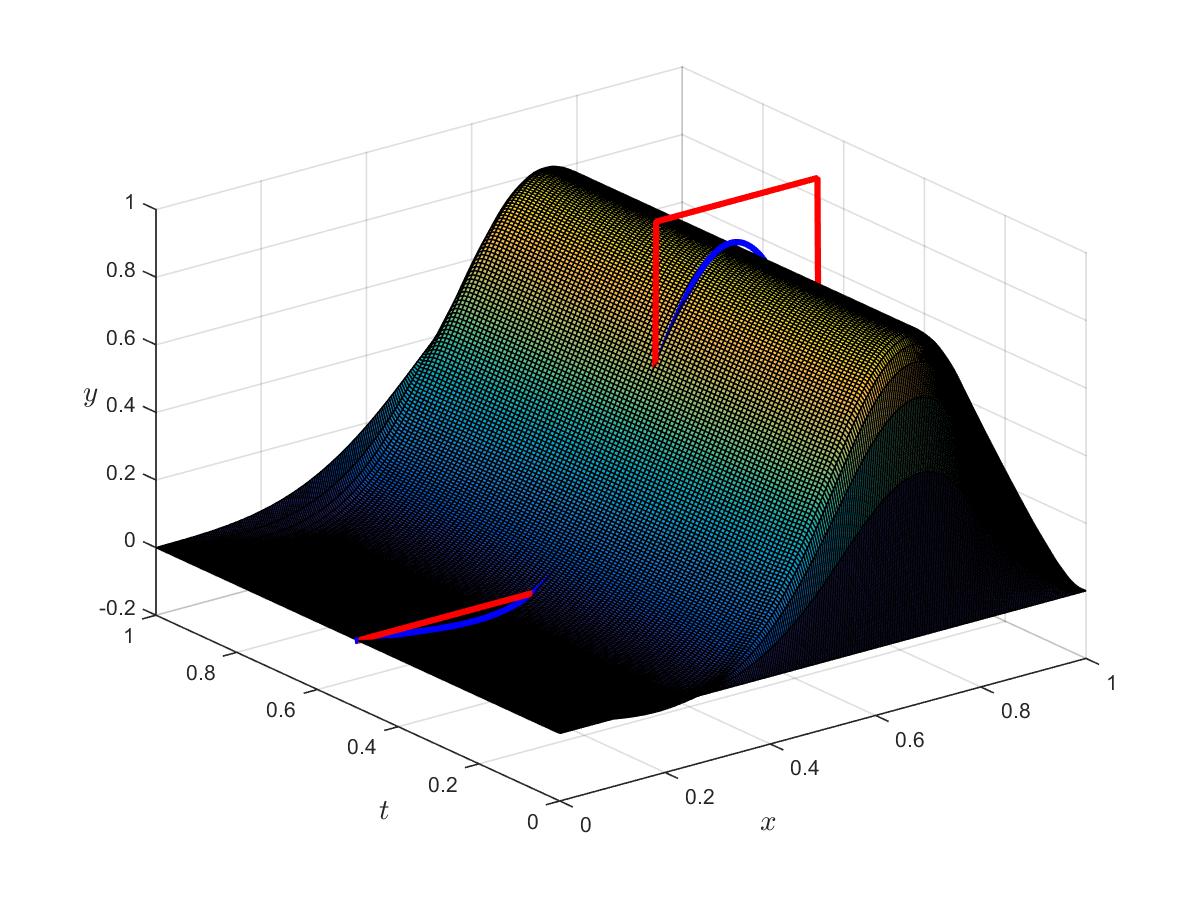Figure 5a: Optimal state for $\alpha_c=\alpha_s=0$ . In red, the target $z$; in blue, the stationary optimal states. 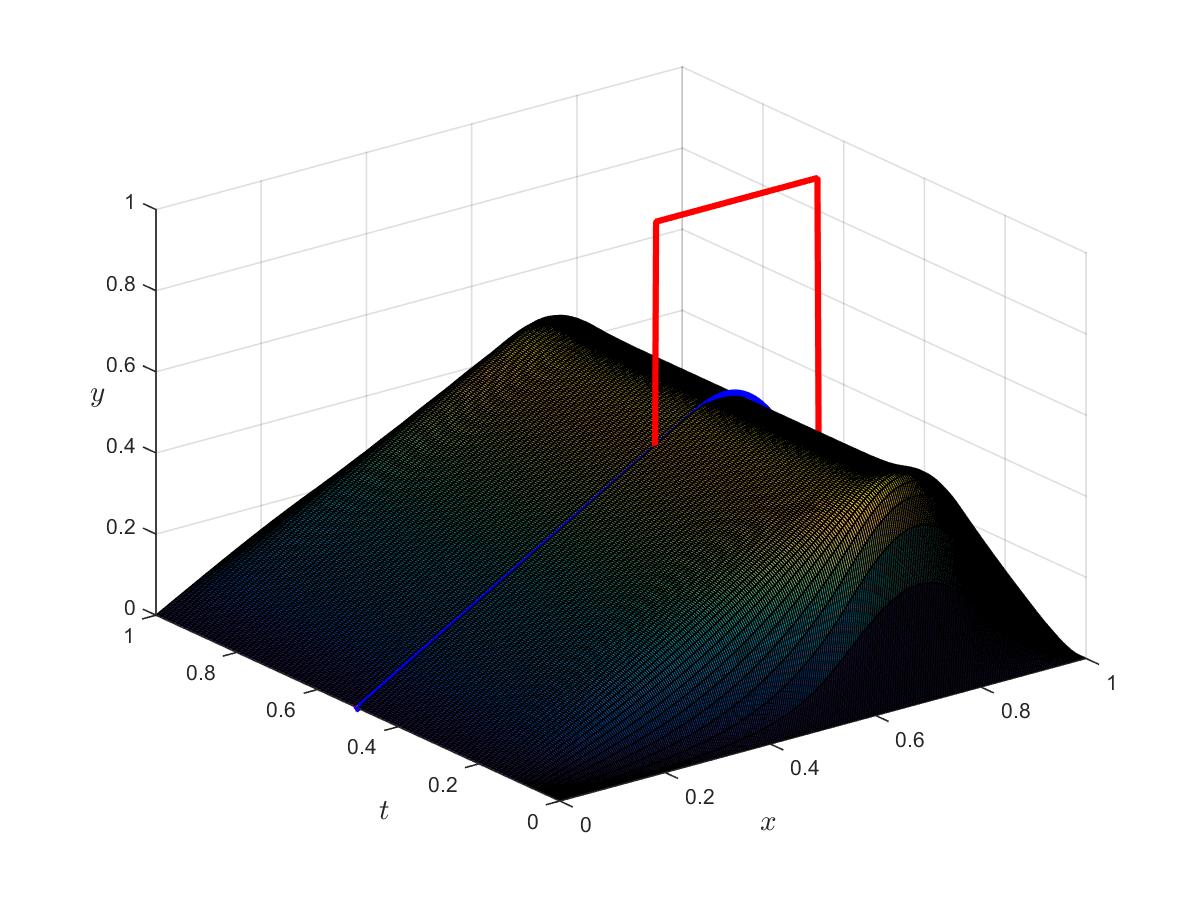Figure 5b: Optimal state for $\alpha_c=0.01$, $\alpha_s=0$. In red, the target $z$; in blue, the stationary optimal states. 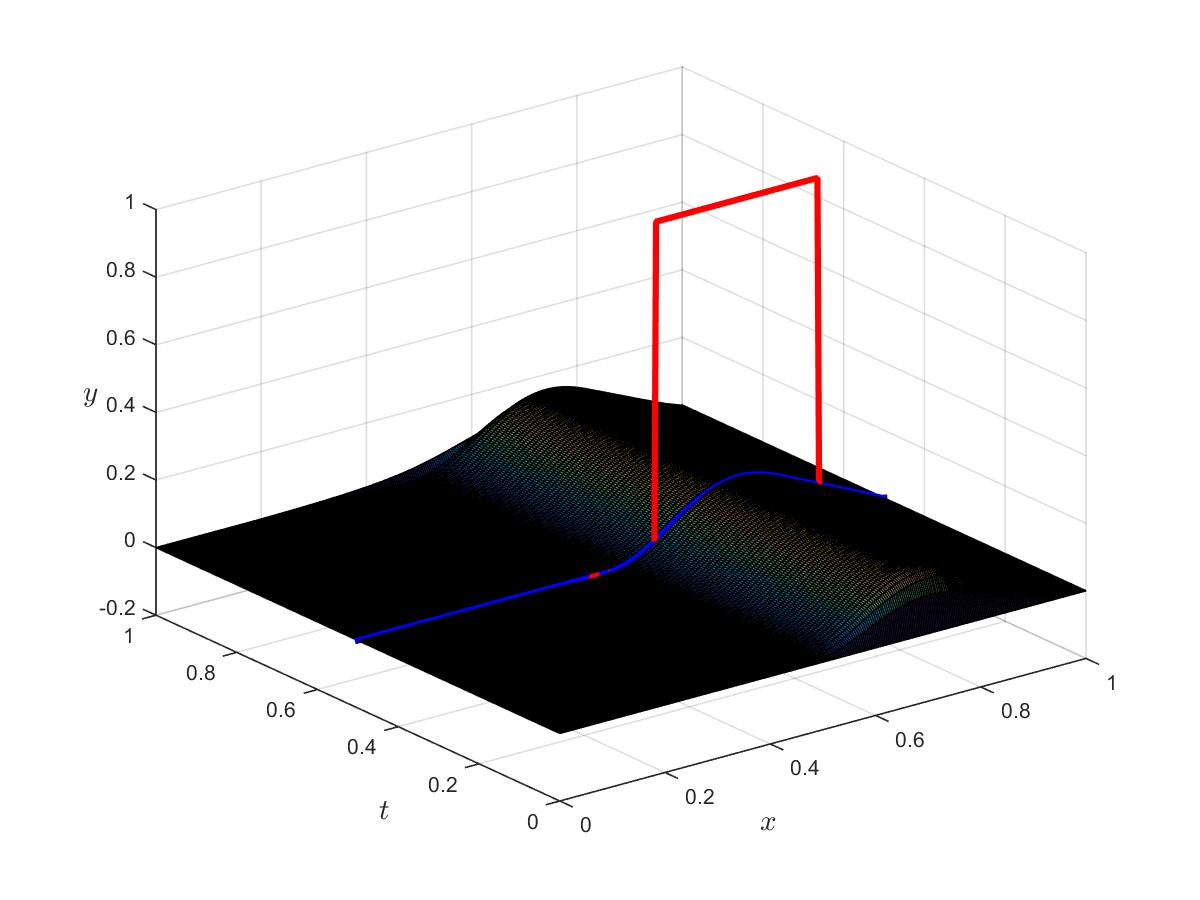Figure 5c: Optimal state for $\alpha_c=0$, $\alpha_s=0.65$. In red, the target $z$; in blue, the stationary optimal states.

Optimal adjoint

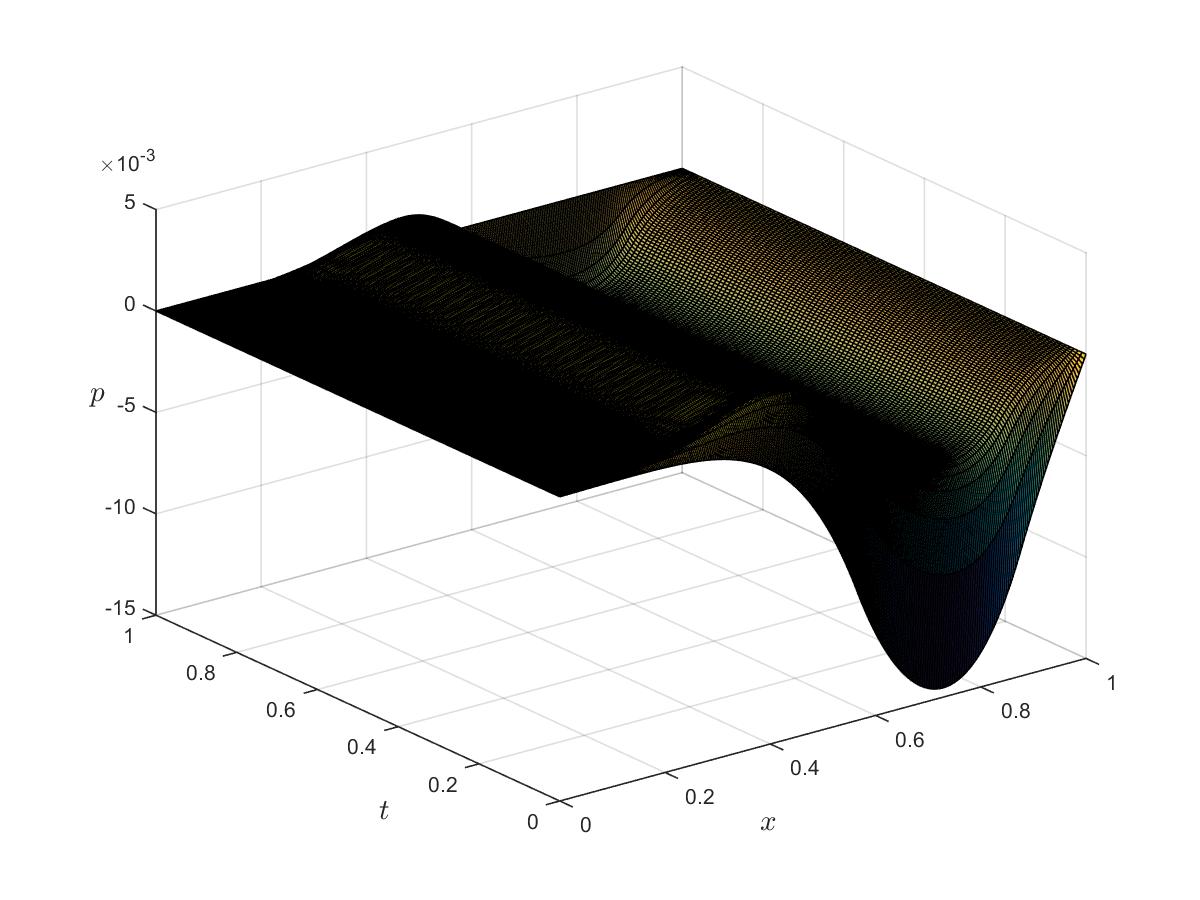Figure 6a: Optimal adjoint for $\alpha_c=\alpha_s=0$. 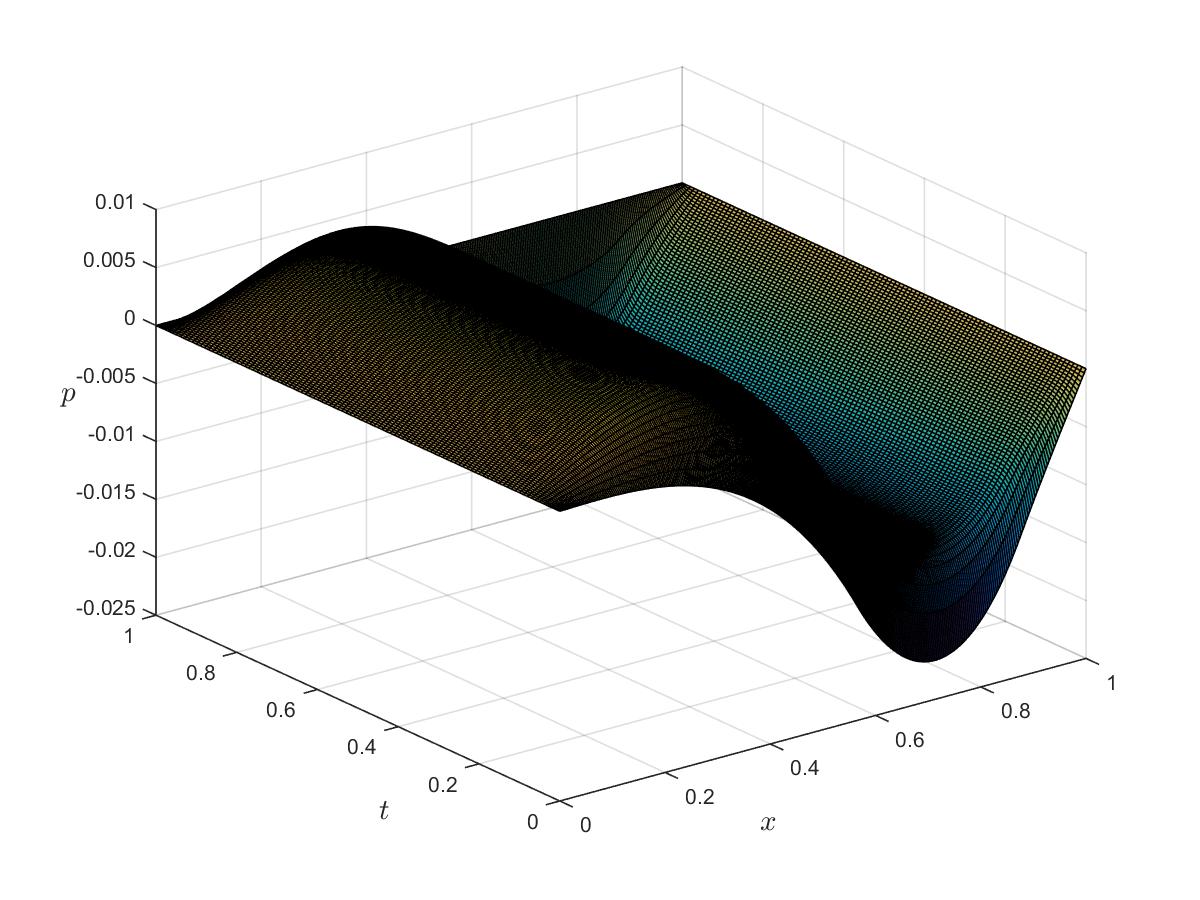Figure 6b: Optimal adjoint for $\alpha_c=0.01$, $\alpha_s=0$. 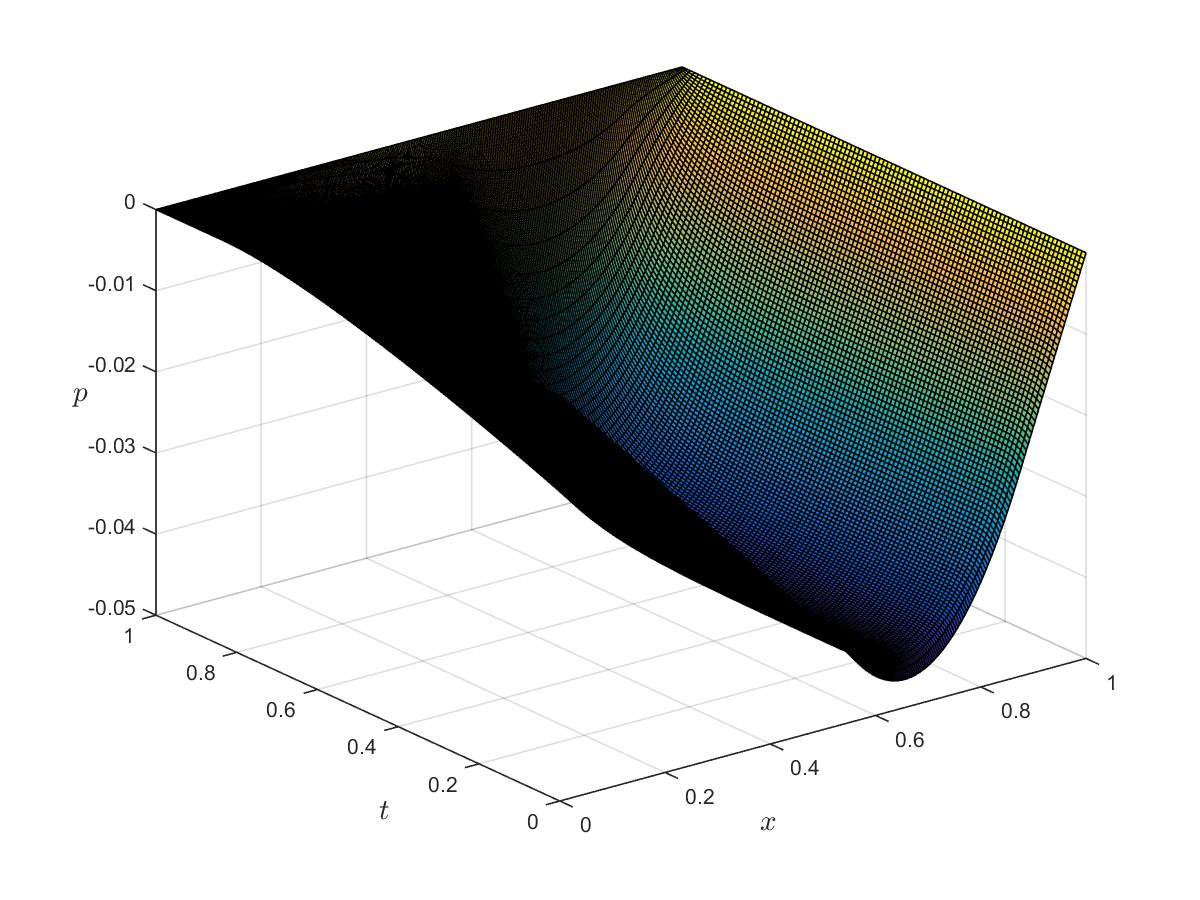Figure 6c: Optimal adjoint for $\alpha_c=0$, $\alpha_s=0.65$.

Bibliography

[1] Peypouquet, J. Convex optimization in normed spaces: theory, methods and examples. With a foreword by Hedy Attouch. Springer Briefs in Optimization. Springer, Cham, 2015. xiv+124 pp.

---